题目内容
【题目】四边形ABCD的对角线AC将其分割成两个三角形:
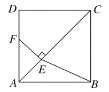
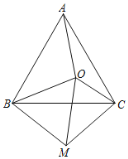
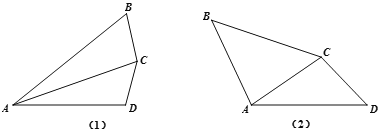
(1)如图1.若∠BAC=∠DAC,AB>AD,求证:AB-AD>CB-CD.
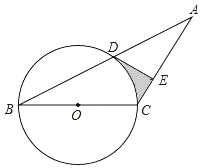
(2)如图2.若∠ACD+∠BAC=180°,∠B=∠D,求证:BC=AD.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)在线段AB上取一点E,使得AE=AD,结合已知条件可以证得△AEC≌△ADC,根据全等的性质得出线段相等,再利用三角形的三边关系:任意两边之差小于第三边即可得出结果;
(2) 过点A作AE垂直于DC的延长线于点E,过点C作CF垂直AB于点F,根据已知条件可证得△CFA≌△AEC,从而证得△BCF≌△DAE,即可得出结果.
(1)证明:如图所示,在线段AB上取一点E,使得AE=AD,
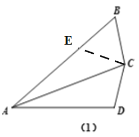
在△AEC和△ADC中
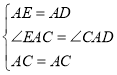
∴△AEC≌△ADC,
∴EC=CD,
∵CB-EC<BE,
∴CB-CD<AB-AE,
∴CB-CD<AB-AD,
∴AB-AD>CB-CD.
(2)证明:如图所示,过点A作AE垂直于DC的延长线于点E,过点C作CF垂直AB于点F
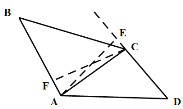
∵∠ACD+∠BAC=180°,∠ACD+∠ACE=180°,
∴∠BAC=∠ACE,
在△ACE和△ACF中
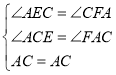
∴△CFA≌△AEC,
∴CF=AE,
在△BCF和△DAE中
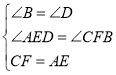
∴△BCF≌△DAE,
∴AD=BC.

练习册系列答案
相关题目