题目内容
【题目】将反比例函数![]() 的图像绕着原点O顺时针旋转45°得到新的双曲线图像
的图像绕着原点O顺时针旋转45°得到新的双曲线图像![]() (如图1所示),直线
(如图1所示),直线![]() 轴,F为x轴上的一个定点,已知,图像
轴,F为x轴上的一个定点,已知,图像![]() 上的任意一点P到F的距离与直线l的距离之比为定值,记为e,即
上的任意一点P到F的距离与直线l的距离之比为定值,记为e,即![]() .
.
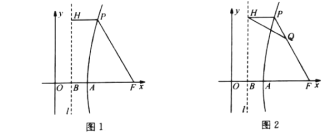
(1)如图1,若直线l经过点B(1,0),双曲线![]() 的解析式为
的解析式为![]() ,且
,且![]() ,则F点的坐标为__________.
,则F点的坐标为__________.
(2)如图2,若直线l经过点B(1,0), 双曲线![]() 的解析式为
的解析式为![]() ,且
,且![]() ,P为双曲线
,P为双曲线![]() 在第一象限内图像上的动点,连接PF,Q为线段PF上靠近点P的三等分点,连接HQ,在点P运动的过程中,当
在第一象限内图像上的动点,连接PF,Q为线段PF上靠近点P的三等分点,连接HQ,在点P运动的过程中,当![]() 时,点P的坐标为__________.
时,点P的坐标为__________.
【答案】F(4,0) ![]()
【解析】
(1)令y=0求出x的值,结合e=2可得出点A的坐标,由点B的坐标及e=2可求出AF的长度,将其代入OF=OB+AB+AF中即可求出点F的坐标;
(2)设点P的坐标为(x,![]() ),则点H的坐标为(1,
),则点H的坐标为(1,![]() ),由Q为线段PF上靠近点P的三等分点,可得出点Q的坐标为(x+
),由Q为线段PF上靠近点P的三等分点,可得出点Q的坐标为(x+![]() ,
,![]() ),利用两点间的距离公式列方程解答即可;
),利用两点间的距离公式列方程解答即可;
解:(1)如图:
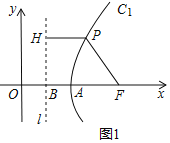
当y=0时,±![]() ,
,
解得:x1=2,x2=-2(舍去),
∴点A的坐标为(2,0).
∵点B的坐标为(1,0),
∴AB=1.
∵e=2,
∴![]() ,
,
∴AF=2,
∴OF=OB+AB+AF=4,
∴F点的坐标为(4,0).
故答案为:(4,0).
(2)设点P的坐标为(x,![]() ),则点H的坐标为(1,
),则点H的坐标为(1,![]() ).
).
∵点Q为线段PF上靠近点P的三等分点,点F的坐标为(5,0),
∴点Q的坐标为(x+![]() ,
,![]() ).
).
∵点H的坐标为(1,![]() ),HQ=
),HQ=![]() HP,
HP,
∴(x+![]() -1)2+(
-1)2+(![]() -
-![]() )2=[
)2=[![]() (x-1)]2,
(x-1)]2,
化简得:15x2-48x+39=0,
解得:x1=![]() ,x2=1(舍去),
,x2=1(舍去),
∴点P的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?