Question

【题目】（问题背景）

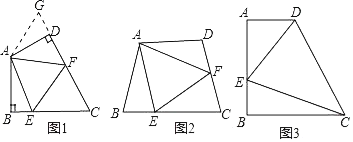
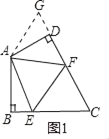
如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，点E、F分别是边BC、CD上的点，且∠EAF＝60°，试探究图中线段BE、EF、FD之间的数量关系．

小王同学探究此问题的方法是：延长FD到点G，使GD＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　 　．

（探索延伸）

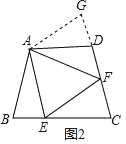
如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．

（学以致用）

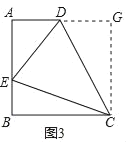
如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝6，E是边AB上一点，当∠DCE＝45°，BE＝2时，则DE的长为　 　．

Answer 1

【答案】【问题背景】：EF＝BE+FD；【探索延伸】：结论EF＝BE+DF仍然成立，见解析；【学以致用】：5.

【解析】

[问题背景]延长FD到点G．使DG＝BE．连结AG，即可证明△ABE≌△ADG，可得AE＝AG，再证明△AEF≌△AGF，可得EF＝FG，即可解题；

[探索延伸]延长FD到点G．使DG＝BE．连结AG，即可证明△ABE≌△ADG，可得AE＝AG，再证明△AEF≌△AGF，可得EF＝FG，即可解题；

[学以致用]过点C作CG⊥AD交AD的延长线于点G，利用勾股定理求得DE的长．

[问题背景】解：如图1，

在△ABE和△ADG中，

∵，

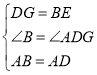∴△ABE≌△ADG（SAS），

∴AE＝AG，∠BAE＝∠DAG，

∵∠EAF＝∠BAD，

∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，

∴∠EAF＝∠GAF，

在△AEF和△GAF中，

∵，

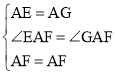∴△AEF≌△AGF（SAS），

∴EF＝FG，

∵FG＝DG+DF＝BE+FD，

∴EF＝BE+FD；

故答案为：EF＝BE+FD．

[探索延伸]解：结论EF＝BE+DF仍然成立；

理由：如图2，延长FD到点G．使DG＝BE．连结AG，

在△ABE和△ADG中，

∵，

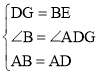∴△ABE≌△ADG（SAS），

∴AE＝AG，∠BAE＝∠DAG，

∵∠EAF＝∠BAD，

∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，

∴∠EAF＝∠GAF，

在△AEF和△GAF中，

∵，

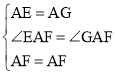∴△AEF≌△AGF（SAS），

∴EF＝FG，

∵FG＝DG+DF＝BE+FD，

∴EF＝BE+FD；

[学以致用]如图3，过点C作CG⊥AD，交AD的延长线于点G，

由【探索延伸】和题设知：DE＝DG+BE，

设DG＝x，则AD＝6﹣x，DE＝x+3，

在Rt△ADE中，由勾股定理得：AD2+AE2＝DE2，

∴（6﹣x）2+32＝（x+3）2，

解得x＝2．

∴DE＝2+3＝5．

故答案是：5．