题目内容
【题目】已知，如图，在ABCD中，延长AB到点E，延长CD到点F，使得BE=DF，连接EF，分别交BC，AD于点M，N，连接AM，CN．
（1）求证：△BEM≌△DFN；
（2）求证：四边形AMCN是平行四边形．
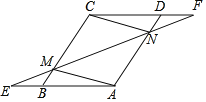
【答案】（1）证明见解析；（2）证明见解析
【解析】
（1）根据平行四边形的性质得出∠BAD=∠BCD，AB∥CD，根据平行线的性质得出∠BAD=∠ADF，∠EBC=∠BCD，∠E=∠F，求出∠ADF=∠EBC，根据全等三角形的判定得出即可；
（2）根据全等求出DN=BM，求出AN=CM，根据平行四边形的判定得出即可．
解：（1）∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，AB∥CD，
∴∠BAD=∠ADF，∠EBC=∠BCD，∠E=∠F，
∴∠ADF=∠EBC，
在△DFN和△BEM中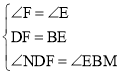
∴△DFN≌△BEM（ASA）；
（2）四边形ANCM是平行四边形，理由是：
∵由（1）知△DFN≌△BEM，
∴DN=BM，
∵四边形ABCD是平行四边形，
∴AD=BC，且AD∥BC，
∴AD﹣DN=BC﹣BM，
∴AN=CM，AN∥CM，
∴四边形ANCM是平行四边形．
练习册系列答案
53天天练系列答案
相关题目
