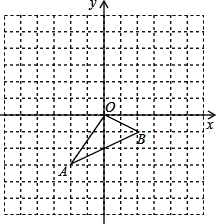
[题目]已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示.则下列结论中.正确的是( )A. ac＜0 B. a+b+c＜0 C. b2﹣4ac＜0 D. b=8a 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（　　）

A. ac＜0 B. a+b+c＜0 C. b2﹣4ac＜0 D. b=8a

【答案】D

【解析】根据二次函数的性质即可得出a，b，c的符号以及a+b+c的值，利用图象与x轴交点个数得出b2﹣4ac符号，以及利用对称轴得出b=8a．

解：∵图象开口向上，对称轴为直线：x=﹣4，

∴a，b同号，

∵图象与y轴交在y轴正半轴上，∴c＞0，

∴A．ac＞0，故此选项错误；

B．当x=1对应的函数图形上x轴上方，所以x=1，y=a+b+c＞0，故此选项错误；

C．∵图象与x轴有两个交点，∴b2﹣4ac＞0，故此选项错误；

D．∵x=﹣=﹣4，

∴b=8a，故此选项正确．

故选：D．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

（1）求商场销售A，B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）

（2）商场准备用不多于2500元的资金购进A，B两种型号计算器共70台，问最少需要购进A型号的计算器多少台？

【题目】问题背景：我们学习了整式的乘法，两个多项式相乘，我们可以运用法则，将其展开，例如：，而将等号的左右两边互换，我们得到了，等号的左边是一个多项式，而右边是几个整式相乘的形式，我们规定将一个多项式写成几个整式相乘的形式，这种运算称之为“因式分解”

问题提出：

如何将进行因式分解呢？

问题探究：

数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题.初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释

例如：我们可以通过表示几何图形面积的方法来快速的对多项式进行因式分解.

如图所示边长为的大正方形是由1个边长为的正方形，2个边长为的长方形，1个边长为的正方形，组成，我们可以用两种方法表示大正方形的面积，这个图形的面积可以表示成：或

∴

我们将等号左边的多项式写成了右边两个整式相乘的形式，从而成功的对多项式进行了因式分解

请你类比上述方法，利用图形的几何意义对多项式进行因式分解（要求自己构图并写出推证过程）

问题拓展：

如何利用图形几何意义的方法推导：？如图，表示1个的正方形，即，表示1个的正方形，与恰好可以拼成1个的正方形，因此：、、就可以表示2个的正方形，即，而、、、恰好可以拼成一个的大正方形.由此可得：

尝试解决：

请你类比上述推导过程，利用图形几何意义方法推导出的值.

（要求自己构造图形并写出推证过程）.

解：

归纳猜想：_________________.

【题目】小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题:

(1)小丽买了自动铅笔、记号笔各几支?

(2)若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案?

【题目】如图，在矩形中，，，点E在边AB上，点F是边BC上不与点B、C重合的一个动点，把沿EF折叠，点B落在点处．若，当是以为腰的等腰三角形时，线段的长为__________．

【题目】（问题背景）

如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，点E、F分别是边BC、CD上的点，且∠EAF＝60°，试探究图中线段BE、EF、FD之间的数量关系．

小王同学探究此问题的方法是：延长FD到点G，使GD＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　　．

（探索延伸）

如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．

（学以致用）

如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝6，E是边AB上一点，当∠DCE＝45°，BE＝2时，则DE的长为　　．

【题目】如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）.

（1）求三角形ABO的面积;

（2）作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′　　　、B′　　　；

（3）P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为__________.

【题目】先阅读理解下面的例题，再按要求解答下列问题：

例题：解一元二次不等式.

解∵，∴可化为.

由有理数的乘法法则：两数相乘，同号得正，得：①②

解不等式组①，得，解不等式组②，得

∴的解集为或.

即一元二次不等式的解集为或.

（1）一元二次不等式的解集为____________；

（2）试解一元二次不等式；

（3）试解不等式.

【题目】小华是花店的一名花艺师，她每天都要为花店制作普通花束和精致花束，她每月工作20天，每天工作8小时，她的工资由基本工资和提成工资两部分构成，每月的基本工资为l800元，另每制作一束普通花束可提2元，每制作一束精致花束可提5元．她制作两种花束的数量与所用时间的关系见下表：

制作普通花束（束）	制作精致花束（束）	所用时间（分钟）
10	25	600
15	30	750

请根据以上信息，解答下列问题：

（1）小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟？

（2）2019年11月花店老板要求小华本月制作普通花束的总时间不少于3000分钟且不超过5000分钟，则小华该月收入最多是多少元？此时小华本月制作普通花束和制作精致花束分别是多少束？

试题分类