Question

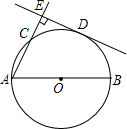如图所示，已知AB为⊙O的直径，C、D是直径AB同侧圆周上两点，且弧CD=弧BD，过D作DE⊥AC于点E，求证：DE是⊙O的切线．

Answer 1

分析：连接OD与BC，交于F点，由弧CD与弧BD相等，利用垂径定理的逆定理得到OD与BC垂直，由垂直的定义得到一个角为直角，再由直径所对的圆周角为直角得到一个直角，由同位角相等两直线平行得到AE与OD平行，再由两直线平行同旁内角互补可得出一对角互补，由AE与ED垂直得到一个角为直角，可得出DE与OD垂直，进而得到DE为圆O的切线．

解答：证明：连接OD，BC，交于点F，如图所示：
∵

CD

=

BD

，OD为圆O的半径，
∴OD⊥BC，
∴∠OFB=90°，
∵AB为圆O的直径，
∴∠ACB=∠OFB=90°，
∴AE∥OD，
∴∠ODE+∠AED=180°，
又AE⊥ED，∴∠AED=90°，
∴∠ODE=90°，
∴DE⊥OD，
则DE为圆O的切线．

点评：此题考查了切线的判定，涉及的知识有：垂径定理的逆定理，以及平行线的判定与性质，切线的判定方法有两种：有点连接证垂直；无点作垂线，证明垂线段等于半径．