题目内容
如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数 的图象在第一象限内的交点,且S△AOB=3.
的图象在第一象限内的交点,且S△AOB=3.(1)该一次函数与反比例函数的解析式是否能完全确定如能确定,请写出它们的解析式;如不能确定,请说明理由.
(2)如果线段AC的延长线与反比例函数的图象的另一支交于D点,过D点作DE⊥x轴于E,那么△ODE的面积与△AOB的面积的大小关系能否确定?
(3)请判断△AOD为何特殊三角形,并证明你的结论.

【答案】分析:(1)根据S△AOB=3可以求出反比例函数的解析式,求出m的值,则一次函数的解析式也相应求出;
(2)根据函数的解析式,就可以通过解方程组求出函数的交点坐标.进而得到两个三角形的面积;
(3)根据A、D的坐标,可以求出AO、DO的长,就可以判断三角形的形状.
解答:解:(1)设B(x,0),则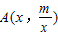 ,其中x>0,m>0,
,其中x>0,m>0,
在Rt△ABO中, ,
,
则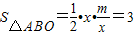 ,即m=6,
,即m=6,
∴一次函数的解析式为y=x+6,
∴反比例函数的解析式为 ;
;
(2)由 得x2+6x-6=0,
得x2+6x-6=0,
解得: ,
,
∴ ,
,
由反比例函数的定义可知,对反比例函数图象上任意一点P(x,y),有 ,即xy=6,
,即xy=6,
∴S△DEO= ×OE×DE=
×OE×DE= ×6=3,
×6=3,
即S△DEO=S△AOB;
(3)由 ,
,
可得 ,
,
即AO=DO,
∵∠AOD>90°,
∴△AOD为钝角等腰三角形.
点评:通过反比例函数图象上的点,作x轴的垂线,垂线,x轴上的点与原点的连线构成的三角形,与反比例函数的解析式的关系.是本题的考查的一个重点.
(2)根据函数的解析式,就可以通过解方程组求出函数的交点坐标.进而得到两个三角形的面积;
(3)根据A、D的坐标,可以求出AO、DO的长,就可以判断三角形的形状.
解答:解:(1)设B(x,0),则
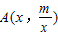 ,其中x>0,m>0,
,其中x>0,m>0,在Rt△ABO中,
 ,
,则
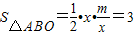 ,即m=6,
,即m=6,∴一次函数的解析式为y=x+6,
∴反比例函数的解析式为
 ;
;(2)由
 得x2+6x-6=0,
得x2+6x-6=0,解得:
 ,
,∴
 ,
,由反比例函数的定义可知,对反比例函数图象上任意一点P(x,y),有
 ,即xy=6,
,即xy=6,∴S△DEO=
 ×OE×DE=
×OE×DE= ×6=3,
×6=3,即S△DEO=S△AOB;
(3)由
 ,
,可得
 ,
,即AO=DO,
∵∠AOD>90°,
∴△AOD为钝角等腰三角形.
点评:通过反比例函数图象上的点,作x轴的垂线,垂线,x轴上的点与原点的连线构成的三角形,与反比例函数的解析式的关系.是本题的考查的一个重点.

练习册系列答案
相关题目
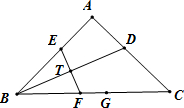 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.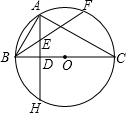 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.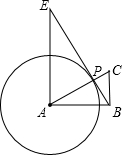 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.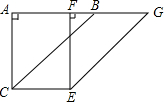 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为