题目内容
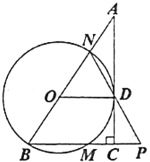
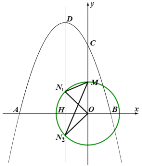
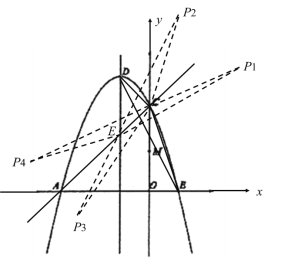
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
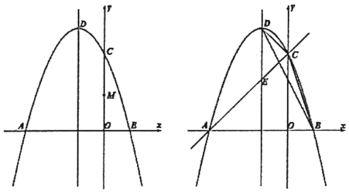
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴正半轴上的一点,
轴正半轴上的一点,![]() ,点
,点![]() 在对称轴左侧的抛物线上运动,直线
在对称轴左侧的抛物线上运动,直线![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,当
是坐标平面内一点,当![]() 与
与![]() 全等时,请直接写出点
全等时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)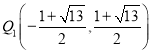 ,
,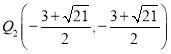 ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)用待定系数法,直接将AB代入解析式即可求解.
(2)由MN平分∠OMD,MD平行ON即可求出OM=ON=![]() ,继而得出N点坐标,由直线ON解析式即可求出与抛物线交点坐标Q即可.
,继而得出N点坐标,由直线ON解析式即可求出与抛物线交点坐标Q即可.
(3)由BCD三点的坐标可得△BCD三角形三边长,由CE坐标可得,△PCE和△ACD中CD=CE,则另两组边对应相等即可,设P点坐标为(x,y);利用勾股定理即列方程求解.
解:(1)∵抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]() .
.
(2)设对称轴与![]() 轴交于点
轴交于点![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ;
;![]() .
.
①当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,
,
依题意得:![]() .
.
解得:![]() ,
,![]() .
.
∵点![]() 在对称轴左侧的抛物线上运动,
在对称轴左侧的抛物线上运动,
∴![]() 点纵坐标
点纵坐标![]() .
.
∴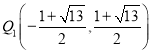 ;
;
②当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,同理可求:
,同理可求:
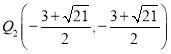 .
.
综上所述:点![]() 的坐标为:
的坐标为:
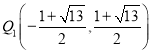 ,
,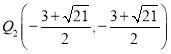
(3)若![]() 与
与![]() 全等,
全等,![]() 点有四个,坐标为
点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
由题意可知:![]() ,
,![]() ,
,![]()
![]() ,B(1,0),
,B(1,0),
![]() ,
,![]() ,
,![]() ,
,
![]() 直线AC经过
直线AC经过![]() ,
,![]() ,设AC的解析式为y=kx+b,
,设AC的解析式为y=kx+b,
将A和C代入,得![]() ,解得:
,解得:![]() ,
,
![]() 直线AC解析式为
直线AC解析式为![]() ,
,
![]() 抛物线对称轴为
抛物线对称轴为![]() ,而直线AC交对称轴于点
,而直线AC交对称轴于点![]() ,
,
![]() 坐标为
坐标为![]() ;
;
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,
,
则![]() ,
,
则![]() ,
,
![]() ,若
,若![]() 与
与![]() 全等,有两种情况,
全等,有两种情况,
Ⅰ.![]() ,
,![]() ,即
,即![]() .
.
![]()
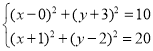 ,
,
解得: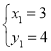 ,
,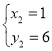 ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
Ⅱ.![]() ,
,![]() ,即
,即![]() .
.
![]()
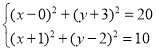 ,
,
解得: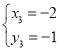 ,
,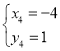 ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
故若△PCE与△ACD全等,P点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目