题目内容
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+x+,则该运动员此次掷铅球,铅球出手时的高度为 .


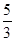 .
.试题分析:先配方,得
y=-
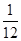 x2+
x2+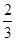 x+
x+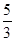
=-
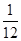 (x-8x)+
(x-8x)+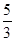
=-
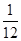 (x-4)2+
(x-4)2+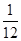 ×16+
×16+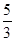
=-
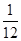 (x-4)2+
(x-4)2+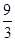

铅球运动员出手时,求高度,即求x=0时,y的取值,y=-
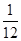 (0-4)2+
(0-4)2+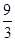 =
=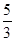 .
.
练习册系列答案
相关题目
题目内容

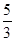 .
.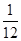 x2+
x2+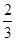 x+
x+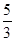
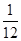 (x-8x)+
(x-8x)+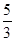
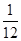 (x-4)2+
(x-4)2+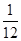 ×16+
×16+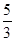
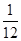 (x-4)2+
(x-4)2+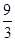

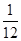 (0-4)2+
(0-4)2+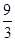 =
=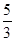 .
.