题目内容
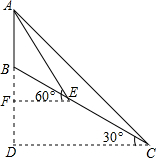
如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)

(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)

(1)233.4cm (2)20.8cm
试题分析:(1)过点B作BE⊥AC于点E,在Rt△ABE中利用三角函数求出AE,由AC=AE﹣CE,可得出答案。
(2)在Rt△ABE中,求出BE,即可计算每级台阶的高度h。
解:如图,过点B作BE⊥AC于点E,

(1)在Rt△ABE中,AB=3m,cos12°≈0.9781,
AE=ABcos12°≈2.934m=293.4cm,
∴AC=AE﹣CE=293.4﹣60=233.4cm。
答:AC的长度约为233.4cm。
(2)h=
 BE=
BE= ABsin12°=
ABsin12°= ×300×0.2079=20.79≈20.8cm,
×300×0.2079=20.79≈20.8cm,答:每级台阶的高度h约为20.8cm。

练习册系列答案
相关题目
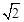 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
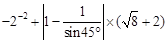 ;
;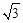 ≈1.73,
≈1.73,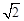 ≈1.41)
≈1.41)
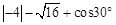 .
.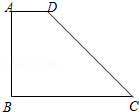
 ,求BC的长和tan∠B的值.
,求BC的长和tan∠B的值.
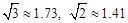 )
)