题目内容
【题目】如图,在Rt△ABC中,![]() ,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至
,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至![]() 时,点
时,点![]() 恰好在同一直线上,此时
恰好在同一直线上,此时![]() 于点E.
于点E.

(1)求证:![]()
(2)若![]() ,求AE的长
,求AE的长
【答案】(1)详见解析;(2)3
【解析】
(1)根据旋转的性质可得AP=AP′,根据等边对等角的性质可得∠APP′=∠AP′P,再根据等角的余角相等证明即可;
(2)过点P作PD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CP=DP,然后求出∠PAD=∠AP′E,利用“角角边”证明△APD和△P′AE全等,根据全等三角形对应边相等可得AE=DP,然后求得AE的长即可;
证明:(1)∵AP′是AP旋转得到,
∴AP=AP′,
∴∠APP′=∠AP′P,
∵∠C=90°,AP′⊥AB,
∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′
∴∠CBP=∠ABP;
(2)如图,过点P作PD⊥AB于D,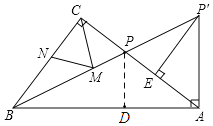
又∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD和△P′AE中,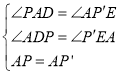 ,
,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP,
∵AB-BC=4,AC=8,
设AB=m,则BC=m-4,
在Rt△PDA中,
![]() ,
,
解得:m=10,
∴AB=10,BC=6,
设PC=PD=x,则AD=10-6=4,PA=8-x,
在R t △PDA中,x2+42=(8-x)2,
解得x=3,
∴AE=CP=3;

练习册系列答案
相关题目





