题目内容
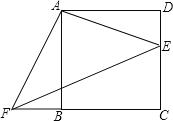
【题目】如图，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．求证：
（1）AB∥CD；
（2）∠2+∠3=90°．
【答案】证明见解析
【解析】
试题分析:（1）首先根据角平分线的定义可得∠ABD=2∠1，∠BDC=2∠2，根据等量代换可得∠ABD+∠BDC=2∠1+2∠2=2（∠1+∠2），进而得到∠ABD+∠BDC=180°，然后根据同旁内角互补两直线平行可得答案；
（2）先根据三角形内角和定理得出∠BED=90°，再根据三角形外角的性质得出∠EDF+∠3=90°，由角平分线的定义可知∠2=∠EDF，代入得到∠2+∠3=90°．
证明：（1）∵DE平分∠BDC（已知），
∴∠ABD=2∠1（ 角平分线的性质）．
∵BE平分∠ABD（已知），
∴∠BDC=2∠2（角的平分线的定义）．
∴∠ABD+∠BDC=2∠1+2∠2=2（∠1+∠2）（ 等量代换）．
∵∠1+∠2=90°（已知），
∴∠ABD+∠BDC=180°（ 等式的性质）．
∴AB∥CD（ 同旁内角互补两直线平行）．
（2）∵∠1+∠2=90°，
∴∠BED=180°﹣（∠1+∠2）=90°，
∴∠BED=∠EDF+∠3=90°，
∵∠2=∠EDF，
∴∠2+∠3=90°．
【题目】某服装店销售一种内衣，每件进价为40元．经过市场调查，一周的销售量y件与销售单价x元/件的关系如表：
销售单价x（元/件） | … | 55 | 60 | 70 | 75 | … |
一周的销售量y（件） | … | 450 | 400 | 300 | 250 | … |
（1）试求出y与x的之间的函数关系式；
（2）设一周的销售利润为S元，请求出S与x的函数关系式，并确定当销售单价的什么范围内变化时，一周的销售利润随着销售单价的增大而增大？
（3）服装店决定将一周的销售内衣的利润全部捐给福利院，在服装店购进该内衣的贷款不超过8000元情况下，请求出该服装店最大捐款数额是多少元？
