题目内容
【题目】两个不相等的实数a，b满足a2+b2=5．
（1）若ab=2，求a+b的值；
（2）若a2﹣2a=m，b2﹣2b=m，求a+b和m的值．
【答案】（1）±3；（2）2，
．
【解析】
（1）先根据完全平方公式求出（a+b）2，再求出即可；
（2）两等式相加、相减，变形后求出a+b=2，再变形后代入a2+b2-2（a+b）=2m，即可求出m．
解：（1）∵a2+b2=5，ab=2，
∴（a+b）2=a2+2ab+b2=5+2×2=9，
∴a+b=±3；
（2）∵a2-2a=m，b2-2b=m，
∴a2-2a=b2-2b，a2-2a+b2-2b=2m，
∴a2-b2-2（a-b）=0，
∴（a-b）（a+b-2）=0，
∵a≠b，
∴a+b-2=0，
∴a+b=2，
∵a2-2a+b2-2b=2m，
∴a2+b2-2（a+b）=2m，
∵a2+b2=5，
∴5-2×2=2m，
解得：m=，
即a+b=2，m=．
【题目】随着我国经济社会的发展，人民对于美好生活的追求越来越高，某社区为了了解家庭对于文化教育的消费情况，随机抽取部分家庭，对每户家庭的文化教育年消费金额进行问卷调查，根据调查结果绘制成如下两幅不完整的统计图表.
级别 | 家庭的文化教育消费金额 | 户数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
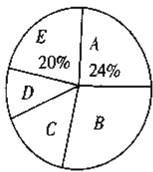
请你根据统计图表提供的信息，解答下列问题：
（1）本次被调查的家庭有___________户，表中
___________；
（2）在扇形统计图中，
组所在扇形的圆心角为多少度？
（3）这个社区有
户家庭，请你估计年文化教育消费在
元以上的家庭有多少户.
【题目】为了解某品牌轿车的耗油情况，将油箱加满后进行了耗油试验，得到如表数据：
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L，行驶150km时，油箱剩余油量为______L；
(2)根据上表的数据，写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式；
(3)某人将油箱加满后，驾驶该轿车从A地前往B地，到达B地时邮箱剩余油量为26L，求A，B两地之间的距离．
