题目内容
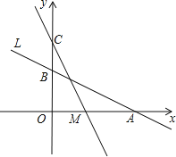
【题目】如图,直线L:![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点
与x轴、y轴分别交于A、B两点,在y轴上有一点![]() ,动点M从A点以每秒1个单位的速度沿x轴向左移动.
,动点M从A点以每秒1个单位的速度沿x轴向左移动.
![]() 求A、B两点的坐标;
求A、B两点的坐标;
![]() 求
求![]() 的面积S与M的移动时间t之间的函数关系式;
的面积S与M的移动时间t之间的函数关系式;
![]() 当t为何值时
当t为何值时![]() ≌
≌![]() ,并求此时M点的坐标.
,并求此时M点的坐标.
【答案】(1)A(0,4),B(0,2);(2)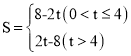 ;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
(1)∵y=﹣![]() x+2,
x+2,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
∴![]() 的面积S与M的移动时间t之间的函数关系式为:
的面积S与M的移动时间t之间的函数关系式为: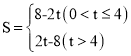
(3)∵OC=OA,∠AOB=∠COM=90°,
∴只需OB=OM,则△COM≌△AOB,
即OM=2,
此时,若M在x轴的正半轴时,t=2,
M在x轴的负半轴,则t=6.
故当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).

【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了如下统计表和统计图(不完整) ,请根据图表中提供的信息解答问题:
得分 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)本次调查的总人数为_______人;
(2)在统计表中,![]() =____,
=____,![]() =__;在扇形统计图中“
=__;在扇形统计图中“![]() ”所在扇形的圆心角的度数为_______
”所在扇形的圆心角的度数为_______
(3)补全频数分布直方图.
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)