题目内容
【题目】在正方形ABCD中,AB=6,对角线AC和BD相交于点O,E是AB所在直线上一点(不与点B重合),将线段OE绕点E顺时针旋转90°得到EF.
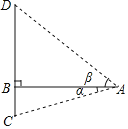
(1)如图1,当点E和点A重合时,连接BF,直接写出BF的长为 ;
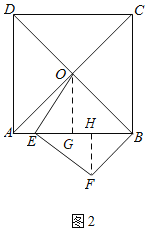
(2)如图2,点E在线段AB上,且AE=1,连接BF,求BF的长;
(3)若DG:AG=2:1,连接CF,H是CF的中点,是否存在点E使△GEH是以EG为直角边的直角三角形?若存在,请直接写出EB的长;若不存在,试说明理由.

【答案】(1)3![]() ;(2)2
;(2)2![]() ;(3)存在,5或
;(3)存在,5或![]() 或
或![]()
【解析】
(1)先根据旋转的性质和正方形的性质得![]() ,再证明
,再证明![]() ,得
,得![]() ;
;
(2)如图2,作辅助线,构建全等三角形,证明![]() ,得
,得![]() ,
,![]() ,计算
,计算![]() 的长,最后利用勾股定理可得结论;
的长,最后利用勾股定理可得结论;
(3)先根据![]() ,且
,且![]() ,计算
,计算![]() ,
,![]() ,分三种情况:①当
,分三种情况:①当![]() 时,
时,![]() 在
在![]() 的左侧时,如图3,作辅助线,构建全等三角形和直角三角形,设
的左侧时,如图3,作辅助线,构建全等三角形和直角三角形,设![]() ,在
,在![]() 中,根据
中,根据![]() ,列方程可得
,列方程可得![]() 的值,从而得
的值,从而得![]() 的长;②当
的长;②当![]() 时,如图4,同理作辅助线,设
时,如图4,同理作辅助线,设![]() ,则
,则![]() ,证明
,证明![]() ,列比例式可得结论,其中
,列比例式可得结论,其中![]() ,就是③,如图5所示,不符合题意.
,就是③,如图5所示,不符合题意.
解:(1)如图1,由旋转得:![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是正方形,且边长为6,
是正方形,且边长为6,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)如图2,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 中,由勾股定理得:
中,由勾股定理得:![]() ;
;
(3)存在![]() 是以
是以![]() 为直角边的直角三角形;
为直角边的直角三角形;
![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,
分三种情况:
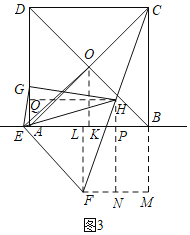
①当![]() 时,
时,![]() 在
在![]() 的左侧时,如图3,过
的左侧时,如图3,过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
设![]() ,
,
同理得![]() ,
,
![]() ,
,![]() ,
,
![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,
时,![]() (如图6所示),
(如图6所示),
当![]() 时,
时,![]() ;
;
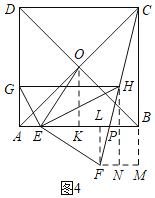
②当![]() 时,如图4,过
时,如图4,过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
设![]() ,则
,则![]() ,
,
同理得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即
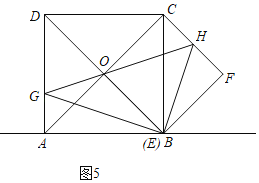
,即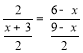 ,
,
![]() ,
,
解得:![]() (舍
(舍![]() 或5,
或5,
即![]() ;
;
③如图5,当![]() 与
与![]() 重合时,
重合时,![]() ,此种情况不符合题意;
,此种情况不符合题意;
综上,![]() 的长是5或
的长是5或![]() 或
或![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】为进一步提升教育教学质量,调动学生学习的兴趣,某校在七年级学生中开展了对语文、数学、英语、历史、地理这五门课程的兴趣爱好情况的调查,以便采取必要教学改革,激发学生对各学科的兴趣爱好.随机选取该年级部分学生进行调查,要求每名学生从中选出一门最感兴趣的课程(每名学生只能选一门,不能多选),以下是根据调查结果绘制的不完整统计图表:
课程代号 |
|
|
|
|
|
课程名称 | 语文 | |数学 | 英语 | 历史 | 地理 |
最感兴趣人数 | 12 | 30 |
| 54 | 9 |
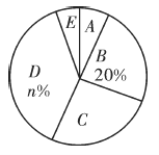
请你根据以上信息,解答下列问题:
(1)被调查学生的总数为______人,![]() ______,
______,![]() ______;
______;
(2)被调查学生中,最喜爱课程的“众数”是______;
(3)若该年级共有800名学生,请估计该年级对语文最感兴趣的学生人数.
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
最受欢迎兴趣班调查问卷 | 统计表 | |||||
选项 | 兴趣班 | 请选择 | 兴趣班 | 频数 | 频率 | |
A | 绘画 | A | 0.35 | |||
B | 音乐 | B | 18 | 0.30 | ||
C | 舞蹈 | C | 15 |
| ||
D | 跆拳道 | D | 6 | |||
你好!请选择一个(只能选一个)你最喜欢的兴趣班,在其后空格内打“√”,谢谢你的合作. |
| 1 | ||||
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从A、B、C、D四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.