题目内容
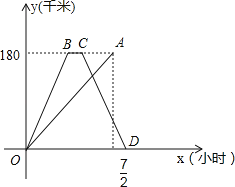
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早
小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：
（1）请直接写出快、慢两车的速度；
（2）求快车返回过程中y（千米）与x（小时）的函数关系式；
（3）两车出发后经过多长时间相距90千米的路程？
【答案】（1）快车、慢车速度分别为120千米/时，60千米/时；（2）y=﹣120x+420（2≤x≤
）；（3）两车出发后经过
或
或
小时相距90千米的路程
【解析】试题分析：（1）根据路程与相应的时间，求得慢车的速度，再根据慢车速度是快车速度的一半，求得快车速度；
（2）先求得点C的坐标，再根据点D的坐标，运用待定系数法求得CD的解析式；
（3）分三种情况：在两车相遇之前；在两车相遇之后；在快车返回之后，分别求得时间即可．
试题解析：
（1）快车速度：180×2÷（
）=120千米/时，
慢车速度：120÷2=60千米/时；
（2）快车停留的时间：
﹣
×2=
（小时），
+=2（小时），即C（2，180），
设CD的解析式为：y=kx+b，则
将C（2，180），D（
，0）代入，得
，
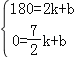解得
，
∴快车返回过程中y（千米）与x（小时）的函数关系式为y=﹣120x+420（2≤x≤
）；
（3）相遇之前：120x+60x+90=180，
解得x=
；
相遇之后：120x+60x﹣90=180，
解得x=
；
快车从甲地到乙地需要180÷120=小时，
快车返回之后：60x=90+120（x﹣﹣）
解得x=
综上所述，两车出发后经过
或
或
小时相距90千米的路程.
