题目内容
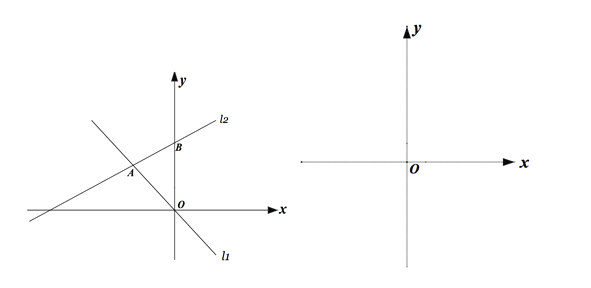
【题目】如图,在平面直角坐标系中，直线l1的解析式为y=-x，直线l2与l1交于A点（a，-a）与，与y轴交于点B（0，b），其中a，b满足（a+2）2+
=0 .
(1)求直线l2放入解析式；
(2)在平面直角坐标系中第二象限有一点P（m，5），使得S△AOP=S△AOB，请求出点P的坐标；
(3)已知平行于y轴且位于y轴左侧有一动直线，分别与
， 
交于点M、N，且点M在点N的下方，点Q为y轴上一动点，且△MNQ为等腰直角三角形，请直接写出满足条件的点Q的坐标.
【答案】(1) y=
x+3（2）P1（-2，5）P2(-8,5)（3）Q1（0， 
）Q2（0， 
）Q3（0， 
）.
【解析】试题分析：（1）根据已知求出A、B两点坐标，然后利用待定系数法即可求出l2的解析式；
（2）由S△BAO=S△PAO，可知点P到AO的距离与点B到AO的距离相等，且点P位于l1两侧，分情况讨论即可得；
（3）设动直线为x=t，由题可得-2<t<0，分三种情况讨论即可得.
试题解析：(1)由题意得：a+2=0，b+3=0，所以a=-2，b=3，
则点A（-2，2），B（0，3），
设l2的解析式为y=kx+3，代入（-2，2），2=-2k+3，解得k=
，
∴l2的解析式为:y=
x+3；
（2）∵S△BAO=S△PAO，则点P到AO的距离与点B到AO的距离相等，且点P位于l1两侧；
当点P在l1的右侧时，设点P为P1，且P1B//l1，
则P1B的解析式为：y=-x+3，
由
得：P1（-2，5），
当点P在l1的左侧时，设点P为P2，
设直线y=5与l1，交于点M，则点M(-5，5)，且点M为P1P2中点，则P2(-8，5)，
综上：P1（-2，5）P2(-8，5)；
（3）设动直线为x=t，由题可得-2<t<0，
则M（t，-t），N（t， 
t+3）)，MN =
t+3，
当NM⊥NQ且NM=NQ时，Q(0， 
t+3)由
t+3=-t，解得t=
，此时Q1（0， 
），
当MN⊥MQ且MN=MQ时，Q(0，-t)由
t+3=-t，解得t=
，此时Q2（0， 
）
当QN⊥QM且QN=QM时，Q(0， 
)，由
=-2t，解得t=
，
此时Q3（0， 
）
综上，Q1（0， 
），Q2（0， 
），Q3（0， 
）.
