题目内容
【题目】如图，在菱形ABCD中，∠A=110°，点E是菱形ABCD内一点，连结CE绕点C顺时针旋转110°，得到线段CF，连结BE，DF，若∠E=86°，求∠F的度数．
【答案】86°．
【解析】试题分析：由菱形的性质有BC=CD，∠BCD=∠A=110°，根据旋转的性质知CE=CF，∠ECF=∠BCD=110°，于是得到∠BCE=∠DCF=110°﹣∠DCE，根据三角形的判定证得△BCE≌△DCF，根据三角形的性质即可得到结论．
试题解析：解：∵菱形ABCD，∴BC=CD，∠BCD=∠A=110°，由旋转的性质知，CE=CF，∠ECF=∠BCD=110°，∴∠BCE=∠DCF=110°﹣∠DCE，在△BCE和△DCF中，∵BC=CD，∠BCE=∠DCF，CE=CF，∴△BCE≌△DCF，∴∠F=∠E=86°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
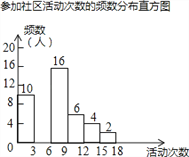
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0＜x≤3 | 10 | 0.20 |
3＜x≤6 | a | 0.24 |
6＜x≤9 | 16 | 0.32 |
9＜x≤12 | 6 | 0.12 |
12＜x≤15 | m | b |
15＜x≤18 | 2 | n |
根据以上图表信息，解答下列问题：
（1）表中a= ，b= ；
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
（3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？
