Question

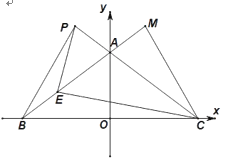
【题目】如图，在平面直角坐标系中，点是轴上一点，点、在轴上，且、满足等式.

（1）求、的值；

（2）若点坐标为，动点从点出发沿射线运动，连接，设点的纵坐标为，的面积为，求与的关系式，并直接写出的取值范围；

（3）当点在线段上，点是线段的延长线上一点，连接、，，若与的周长差为 2，点是轴上一点，若是以为顶角的等腰三角形，求点的坐标．

Answer 1

【答案】（1），；（2）当点在线段上时，，当点在线段延长线上时，；（3）点或．

【解析】

（1）根据平方和绝对值的非负性，可求出、的值；

（2）根据A、B、C三点坐标，可求出，过点作轴，垂足为，所以，所以，由此可分情况讨论：当点在线段上时：，

当点在线段延长线上时：.

（3）延长至点，使，连接，根据题意先证出，然后可得，，所以，设，，所以，由与的周长差为 2，可求出，因为是以为顶角的等腰三角形，所以，故可得Q点坐标.

（1）因为，所以，

因为，，所以， ，所以，.

（2）因为，，所以，因为，所以，

所以，过点作轴，垂足为，

所以，所以，

当点在线段上时：，

当点在线段延长线上时：.

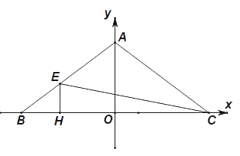
（3）设，所以，设，

所以，所以，

延长至点，使，连接，

因为，，

所以，

，

因为，所以，

所以，设，，

所以，因为与的周长差为 2，

所以，因为，所以，

因为是等腰三角形，所以，所以或，所以点或．