题目内容
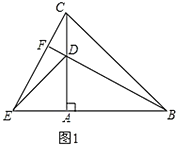
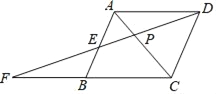
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).

(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
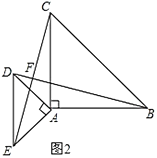
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且![]() ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示).
【答案】(1)![]() cm;(2)当t=1或
cm;(2)当t=1或![]() 秒时,△PCQ与△ACB相似;(3)CE=3+t;
秒时,△PCQ与△ACB相似;(3)CE=3+t;
【解析】
(1)利用勾股定理可求得AB.
(2)分![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(3) 过点![]() 作
作![]() 交
交![]() 于
于![]() ,先说明△
,先说明△![]() ∽△
∽△![]() ,得到
,得到![]() ,用含t的代数式表示HE、CH,最后用勾股定理求出CE.
,用含t的代数式表示HE、CH,最后用勾股定理求出CE.
(1)AB=![]() cm;
cm;
(2)由题意可知:![]() ,
,![]() ,QC=5-t
,QC=5-t
∵∠PCQ=∠ACB
∴当![]() 或
或![]() 时,△PCQ与△ACB相似
时,△PCQ与△ACB相似
当![]() 时,
时,![]() ,解得t=1;
,解得t=1;
当![]() 时,
时,![]() ,解得t=
,解得t=![]() ,
,
![]() 当t=1或
当t=1或![]() 秒时,△PCQ与△ACB相似;
秒时,△PCQ与△ACB相似;
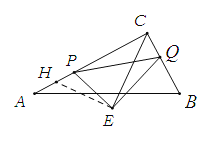
(3)如图,过点![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]()
![]()
![]() 即
即![]()
∴![]()
∵![]()
∴![]()
![]() △
△![]() ∽△
∽△![]()
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 中,
中,![]() ,
,
即![]()
∴![]()
∴![]()
故答案为:(1)![]() cm;(2)当t=1或
cm;(2)当t=1或![]() 秒时,△PCQ与△ACB相似;(3)CE=3+t.
秒时,△PCQ与△ACB相似;(3)CE=3+t.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目