Question

【题目】已知：AF平分∠BAE，CF平分∠DCE．

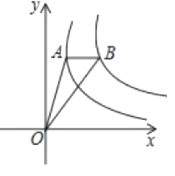
（1）如图①，已知AB∥CD，求证：∠AEC=∠C－∠A；

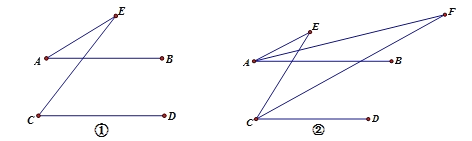
（2）如图②，在（1）的条件下，直接写出∠E与∠F的关系．

∠E=　　　　 （用含有∠F的式子表示）

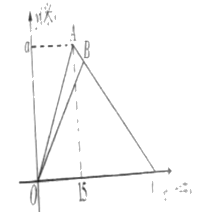
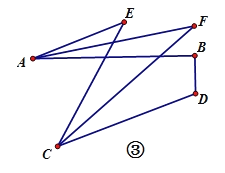
（3）如图③，BD⊥AB，垂足为B，∠BDC=110°，∠AEC=40°，求∠AFC的度数．

Answer 1

【答案】（1）证明见解析；（2）∠E=2∠F；（3）30°

【解析】

（1）根据平行线的性质推出同位角相等，再根据三角形的外角性质得出结论即可；

（2）根据AF平分∠EAB，CF平分∠ECD，可得∠ECD=2∠FCD，∠EAB=2∠FAM，根据AB∥CD，可得∠FNB=∠FCD，∠EGN=∠ECD，进而证明∠E=2∠F；

（3）如图③，设∠EAM=x°，∠ECD=y°，则可求出∠BMC=140°-x°，由四边形内角和可得∠BMC+∠DCM=160°,从而可得y°-x°=20°；再根据△AEN和△FCN的外角可得∠F+y°=40°+x°，从而可求出∠F的值.

（1）如图①，

∵AB∥CD，

∴∠EMB=∠ECD，

∵∠AEC+∠EAB=∠EBM，

∴∠AEC+∠EAB=∠ECD，

∴∠AEC=∠C－∠A；

（2）如图②，

（2）∵AF平分∠EAB，CF平分∠ECD，

∴∠ECD=2∠FCD，∠EAB=2∠FAB，

∵AB∥CD，

∴∠FNB=∠FCD，∠EGB=∠ECD，

∵∠FNB是△ANF的外角，

∴∠F=∠FNB-∠FAN=∠FCD-∠FAN

=∠ECD-∠EAB=∠EGN-∠EAB=（∠EGN-∠EAB）=∠E，

即∠E=2∠F；

（3）如图③，

设∠EAM=x°，∠ECD=y°，

则∠AME=180°-x°-40°=140°-x°,

即∠BMC=140°-x°，

在四边形BDCM中，∠B=90°，∠BDC=110°，

∴∠BMC+∠DCM=360°-∠B-∠BDC=360°-90°-110°=160°,

∴140°-x°+y°=160°，

∴y°-x°=20°，

∵AF平分∠BAE，CF平分∠DCE，

∴∠EAN=∠EAM=x°，∠FCN=∠DCM=y°，

在△ANE和△FCN中，∠ENF=40°+x°，∠ENF=∠F+y°，

∴∠F+y°=40°+x°，

∴∠F=40°+x°-y°=40°-(y°-x°)=40°-×20°=30°.