Question

【题目】关于二次函数y=2x2﹣mx+m﹣2，以下结论：

①抛物线交x轴有交点；

②不论m取何值，抛物线总经过点（1，0）；

③若m＞6，抛物线交x轴于A、B两点，则AB＞1；

④抛物线的顶点在y=﹣2（x﹣1）2图象上．其中正确的序号是（　　）

A. ①②③④ B. ①②③ C. ①②④ D. ②③④

Answer 1

【答案】A

【解析】二次函数y=2x2-mx+m-2，

∵a=2，b=-m，c=m-2，

∴b2-4ac=（-m）2-8（m-2）=（m-4）2≥0，

则抛物线与x轴有交点，故①正确；

∵当x=1时，y=2-m+m-2=0，

∴不论m取何值，抛物线总经过点（1，0），故②正确；

设A的坐标为（x1，0），B（x2，0），

令y=0，得到2x2-mx+m-2=0，

∴x1+x2=，x1x2=，

∴AB=|x1-x2|=|，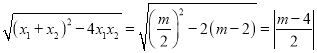

当m＞6时，可得m-4＞2，即＞1，

∴AB＞1，故③正确；

∵抛物线的顶点坐标为（， ），

∴将x=代入得：y=-2（-1）2=-2（）=，

∴抛物线的顶点坐标在y=-2（x-1）2图象上，故④正确，

综上，正确的序号有①②③④，

故选A.