Question

【题目】如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．
（1）求证：△ACD≌△EDC；
（2）请探究△BDE的形状，并说明理由．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，

由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，

∴AD=EC，

在△ACD和△EDC中， ，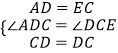

∴△ACD≌△EDC（SAS）

（2）解：△BDE是等腰三角形；理由如下：

∵AC=BD，DE=AC，

∴BD=DE，

∴△BDE是等腰三角形

【解析】（1）由矩形的性质得出AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，得出AD=EC，由SAS即可得出结论；（2）由AC=BD，DE=AC，得出BD=DE即可．
【考点精析】利用矩形的性质和平移的性质对题目进行判断即可得到答案，需要熟知矩形的四个角都是直角，矩形的对角线相等；①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等．