��Ŀ����
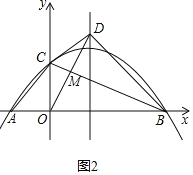
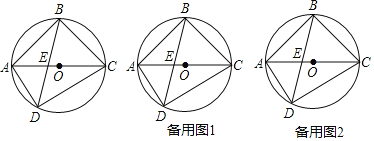
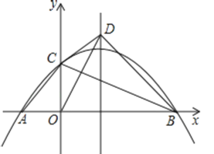
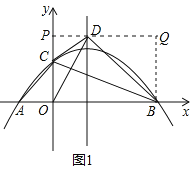
����Ŀ����ƽ��ֱ������ϵ�У�������y��mx2��2mx��3m��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C������AC��BC������OBC��BC���ڵ�ֱ�߷��ۣ��õ���DBC������OD��
��1����A�������� ������B�������� ����
��2����ͼ������D���������ߵĶԳ����ϣ�����x���Ϸ����������ߵĽ���ʽ��
��3������OBD�����ΪS1����OAC�����ΪS2����S1��![]() S2����m��ֵ��
S2����m��ֵ��
���𰸡���1��(��1��0)��(3��0)����2��y����![]() x2+
x2+![]() x+
x+![]() ����3����
����3����![]()
��������
��1�������ߵı���ʽΪ��y��m��x2��2x��3����m��x+1����x��3����������⣻
��2��֤����CPD�ס�DQB��������⣻
��3��S2��S��AOC��![]() ��1������3m����-
��1������3m����-![]() m����S1��S��BOD��
m����S1��S��BOD��![]() ��DO��MB��OM��MB����S1��
��DO��MB��OM��MB����S1��![]() S2�������.
S2�������.
��1�������ߵı���ʽΪ��y��m��x2��2x��3����m��x+1����x��3����
�ʵ�A��B������ֱ�Ϊ������1��0������3��0����
�ʴ�Ϊ������1��0������3��0����
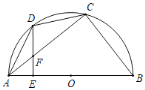
��2������B��y���ƽ����BQ������D��x���ƽ���߽�y���ڵ�P����BQ�ڵ�Q��
�裺D��1��n������C��0����3m����
�ߡ�CDP+��PDC��90������PDC+��QDB��90����
���QDB����DCP��
�֡ߡ�CPD����BQD��90����
���CPD�ס�DQB��
��![]() ,
,
����CP��n+3m��DQ��3��1��2��PD��1��BQ��n��CD����3m��BD��3��
��������ֵ�������ʽ����ã�m����![]() ��
��
��m��0����m����![]() ��
��
�������ߵı���ʽΪ��y����![]() x2+
x2+![]() x+
x+![]() ��
��
��3��y��m��x2��2x��3����m��x+1����x��3����
��C��0����3m����CO����3m��
��A����1��0����B��3��0����
��AB��4��
��S2��S��AOC��![]() ��1������3m������
��1������3m������![]() m��
m��
��OD��BC�ڵ�M��
����Գ��ԣ�BC��OD��OD��2OM��
��Rt��COB��BC��![]() ,
,
��������ã�OM�� ![]() ,
,
��tan��COB��![]() ����m����cos��COB��
����m����cos��COB��![]() ,
,
MB��OBcos��COB��![]() ,
,
��S1��S��BOD��![]() ��DO��MB��OM��MB����
��DO��MB��OM��MB����![]() ,
,
��S1��![]() S2��
S2��
��m2+1��![]() ��m��0����
��m��0����
��m����![]() .
.