题目内容
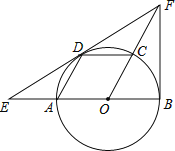
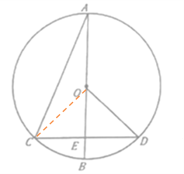
【题目】如图,在圆O中,直径AB平分弦CD于点E,且CD=4![]() ,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )
,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )

A.2![]() B.4C.
B.4C.![]() D.2
D.2
【答案】D
【解析】
连接CO,由直径AB平分弦CD及垂径定理知∠COB=∠DOB,则∠A与∠COB互余,由圆周角定理知∠A=30°,∠COE=60°,则∠OCE=30°,设OE=x,则CO=2x,利用勾股定理即可求出x,再求出BE即可.
连接CO,∵AB平分CD,
∴∠COB=∠DOB,AB⊥CD,CE=DE=2![]()
∵∠A与∠DOB互余,
∴∠A+∠COB=90°,
又∠COB=2∠A,
∴∠A=30°,∠COE=60°,
∴∠OCE=30°,
设OE=x,则CO=2x,
∴CO2=OE2+CE2
即(2x)2=x2+(2![]() )2
)2
解得x=2,
∴BO=CO=4,
∴BE=CO-OE=2.
故选D.

练习册系列答案
相关题目