题目内容
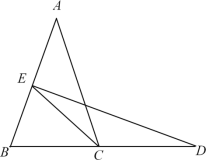
【题目】已知:如图,四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 边匀速运动,运动速度为
边匀速运动,运动速度为![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 边匀速运动,运动速度为
边匀速运动,运动速度为![]() .点
.点![]() 和点
和点![]() 同时出发,
同时出发,![]() 为四边形
为四边形![]() 的对角线的交点,连接
的对角线的交点,连接![]() 并延长交
并延长交![]() 于
于![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积等于五边形
的面积等于五边形![]() 面积的
面积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
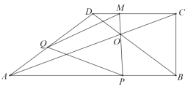
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)不存在,理由详见解析;(4)存在,
;(3)不存在,理由详见解析;(4)存在,![]() ,
,![]() .
.
【解析】
(1)如下图,根据Rt△ADH求得AD的长,在利用QP∥DB得到t的值;
(2)先利用![]() ,得到AP、BP、DM,然后用割补法求面积;
,得到AP、BP、DM,然后用割补法求面积;
(3)假设存在,使得![]() 的面积等于五边形面积的
的面积等于五边形面积的![]() ,验证t的值是否在取值范围内;
,验证t的值是否在取值范围内;
(4)如下图,分别在Rt△EMQ和Rt△QFP中求得QM和QP的长,令它们相等求得t.
(1)如下图,过点D作AB的垂线交AB于点H
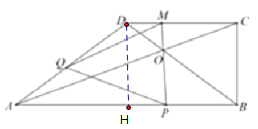
∵DC=8,AB=16,CB=6,∴AH=8,DH=6
∴在Rt△DHA中,![]()
设![]() 则
则![]()
∴![]()
∵QP∥DB
![]() ,即
,即![]()
解得:![]() .
.
(2)∵DC∥AB
∴∠ABO=∠CDO,∠OAB=∠DCO
∴![]()
∴![]()
∵![]() ,∴
,∴![]()
![]()
∴![]() 四
四![]()
![]()
![]()
![]() .
.
(3)∵![]() 四
四![]()
![]()
又∵![]() 的面积等于五边形面积的
的面积等于五边形面积的![]()
∴![]() 四
四![]() ,即:
,即:![]()
解得:![]() ,
,![]()
![]() ,
,![]() 不存在.
不存在.
(4)如下图,延长CD,过点Q作AB的垂线,交CD于点E,AB与点F
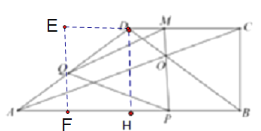
∵∠QAF=QDE,∠AHD=∠QED
∴△AHD∽△DEQ
同理,△ADH∽△AQF
∵AD=10,AH=8
又∵QD=t
∴EQ=![]() ,ED=
,ED=![]()
∵AQ=10-t
∴AF=![]() ,FQ=
,FQ=![]()
∴QM=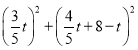
QP=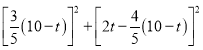
∵点Q是MP的垂直平分线,∴QM=QP,即:
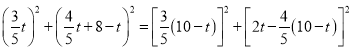
化简得:![]()
解得:![]() ,
,![]() .
.

【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
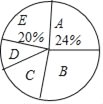
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?