ЬтФПФкШн
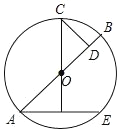
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌОиаЮABCDЕФБпABЃН4ЃЌBCЃН6ЃЎШєВЛИФБфОиаЮABCDЕФаЮзДКЭДѓаЁЃЌЕБОиаЮЖЅЕуAдкxжсЕФе§АыжсЩЯзѓгввЦЖЏЪБЃЌОиаЮЕФСэвЛИіЖЅЕуDЪМжедкyжсЕФе§АыжсЩЯЫцжЎЩЯЯТвЦЖЏЃЎ
(1)ЕБЁЯOADЃН30ЁуЪБЃЌЧѓЕуCЕФзјБъЃЛ
(2)ЩшADЕФжаЕуЮЊMЃЌСЌНгOMЁЂMCЃЌЕБЫФБпаЮOMCDЕФУцЛ§ЮЊ![]() ЪБЃЌЧѓOAЕФГЄЃЛ
ЪБЃЌЧѓOAЕФГЄЃЛ
(3)ЕБЕуAвЦЖЏЕНФГвЛЮЛжУЪБЃЌЕуCЕНЕуOЕФОрРыгазюДѓжЕЃЌЧыжБНгаДГізюДѓжЕЃЌВЂЧѓДЫЪБcosЁЯOADЕФжЕЃЎ

ЁОД№АИЁП(1)ЕуCЕФзјБъЮЊ(2ЃЌ3+2![]() )ЃЛ(2)OAЃН3
)ЃЛ(2)OAЃН3![]() ЃЛ(3)OCЕФзюДѓжЕЮЊ8ЃЌcosЁЯOADЃН
ЃЛ(3)OCЕФзюДѓжЕЮЊ8ЃЌcosЁЯOADЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)зїCEЁЭyжсЃЌЯШжЄЁЯCDEЃНЁЯOADЃН30ЁуЕУCEЃН![]() CDЃН2ЃЌDEЃН
CDЃН2ЃЌDEЃН![]() ЃЌдйгЩЁЯOADЃН30ЁужЊODЃН
ЃЌдйгЩЁЯOADЃН30ЁужЊODЃН![]() ADЃН3ЃЌДгЖјЕУГіЕуCзјБъЃЛ
ADЃН3ЃЌДгЖјЕУГіЕуCзјБъЃЛ
(2)ЯШЧѓГіSЁїDCMЃН6ЃЌНсКЯSЫФБпаЮOMCDЃН![]() жЊSЁїODMЃН
жЊSЁїODMЃН![]() ЃЌSЁїOADЃН9ЃЌЩшOAЃНxЁЂODЃНyЃЌОнДЫжЊx2+y2ЃН36ЃЌ
ЃЌSЁїOADЃН9ЃЌЩшOAЃНxЁЂODЃНyЃЌОнДЫжЊx2+y2ЃН36ЃЌ![]() xyЃН9ЃЌЕУГіx2+y2ЃН2xyЃЌМДxЃНyЃЌДњШыx2+y2ЃН36ЧѓЕУxЕФжЕЃЌДгЖјЕУГіД№АИЃЛ
xyЃН9ЃЌЕУГіx2+y2ЃН2xyЃЌМДxЃНyЃЌДњШыx2+y2ЃН36ЧѓЕУxЕФжЕЃЌДгЖјЕУГіД№АИЃЛ
(3)гЩMЮЊADЕФжаЕуЃЌжЊOMЃН3ЃЌCMЃН5ЃЌгЩOCЁмOM+CMЃН8жЊЕБOЁЂMЁЂCШ§ЕудкЭЌвЛжБЯпЪБЃЌOCгазюДѓжЕ8ЃЌСЌНгOCЃЌдђДЫЪБOCгыADЕФНЛЕуЮЊMЃЌONЁЭADЃЌжЄЁїCMDЁзЁїOMNЕУ![]() ЃЌОнДЫЧѓЕУMNЃН
ЃЌОнДЫЧѓЕУMNЃН![]() ЃЌONЃН
ЃЌONЃН![]() ЃЌANЃНAMЉMNЃН
ЃЌANЃНAMЉMNЃН![]() ЃЌдйгЩOAЃН
ЃЌдйгЩOAЃН![]() МАcosЁЯOADЃН
МАcosЁЯOADЃН![]() ПЩЕУД№АИЃЎ
ПЩЕУД№АИЃЎ
(1)ШчЭМ1ЃЌЙ§ЕуCзїCEЁЭyжсгкЕуEЃЌ
ЁпОиаЮABCDжаЃЌCDЁЭADЃЌ
ЁрЁЯCDE+ЁЯADOЃН90ЁуЃЌ
гжЁпЁЯOAD+ЁЯADOЃН90ЁуЃЌ
ЁрЁЯCDEЃНЁЯOADЃН30ЁуЃЌ
ЁрдкRtЁїCEDжаЃЌCEЃН![]() CDЃН2ЃЌDEЃН
CDЃН2ЃЌDEЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
дкRtЁїOADжаЃЌЁЯOADЃН30ЁуЃЌ
ЁрODЃН![]() ADЃН3ЃЌ
ADЃН3ЃЌ
ЁрЕуCЕФзјБъЮЊ(2ЃЌ3+2![]() )ЃЛ
)ЃЛ
(2)ЁпMЮЊADЕФжаЕуЃЌ
ЁрDMЃН3ЃЌSЁїDCMЃН6ЃЌ
гжSЫФБпаЮOMCDЃН![]() ЃЌ
ЃЌ
ЁрSЁїODMЃН![]() ЃЌ
ЃЌ
ЁрSЁїOADЃН9ЃЌ
ЩшOAЃНxЁЂODЃНyЃЌдђx2+y2ЃН36ЃЌ![]() xyЃН9ЃЌ
xyЃН9ЃЌ
Ёрx2+y2ЃН2xyЃЌМДxЃНyЃЌ
НЋxЃНyДњШыx2+y2ЃН36ЕУx2ЃН18ЃЌ
НтЕУxЃН3![]() (ИКжЕЩсШЅ)ЃЌ
(ИКжЕЩсШЅ)ЃЌ
ЁрOAЃН3![]() ЃЛ
ЃЛ
(3)OCЕФзюДѓжЕЮЊ8ЃЌ
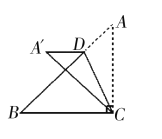
ШчЭМ2ЃЌMЮЊADЕФжаЕуЃЌ
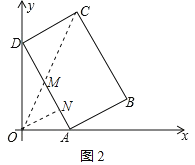
ЁрOMЃН3ЃЌCMЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрOCЁмOM+CMЃН8ЃЌ
ЕБOЁЂMЁЂCШ§ЕудкЭЌвЛжБЯпЪБЃЌOCгазюДѓжЕ8ЃЌ
СЌНгOCЃЌдђДЫЪБOCгыADЕФНЛЕуЮЊMЃЌЙ§ЕуOзїONЁЭADЃЌДЙзуЮЊNЃЌ
ЁпЁЯCDMЃНЁЯONMЃН90ЁуЃЌЁЯCMDЃНЁЯOMNЃЌ
ЁрЁїCMDЁзЁїOMNЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУMNЃН![]() ЃЌONЃН
ЃЌONЃН![]() ЃЌ
ЃЌ
ЁрANЃНAMЉMNЃН![]() ЃЌ
ЃЌ
дкRtЁїOANжаЃЌOAЃН![]() ЃЌ
ЃЌ
ЁрcosЁЯOADЃН![]() ЃЎ
ЃЎ

 ЛЦИдаЁзДдЊНтОіЮЪЬтЬьЬьСЗЯЕСаД№АИ
ЛЦИдаЁзДдЊНтОіЮЪЬтЬьЬьСЗЯЕСаД№АИ Ш§ЕувЛВтПьРжжмМЦЛЎЯЕСаД№АИ
Ш§ЕувЛВтПьРжжмМЦЛЎЯЕСаД№АИ