题目内容
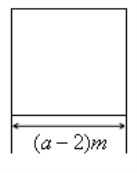
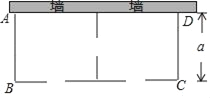
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
【答案】(1)60﹣3a;(2)a=12;(3)当a=11时,y最大=297.
【解析】
(1)用总长减去3a后加上三个1米宽的门即为所求;
(2)由(1)表示饲养场面积计算即可,注意a的范围讨论;
(3)设出饲养场面积y与x之间的函数关系,根据已知条件确定自变量a的范围,求函数最大值.
(1)由已知饲养场的长为57﹣2a﹣(a﹣1)+2=60﹣3a;
故答案为:60﹣3a;
(2)由(1)饲养场面积为a(60﹣3a)=288,
解得a=12或a=8;
当a=8时,60﹣3a=60﹣24=36>27,
故a=8舍去,
则a=12;
(3)设饲养场面积为y,
则y=a(60﹣3a)=﹣3a2+60a=﹣3(a﹣10)2+300,
∵2<60﹣3a≤27,
∴11≤a<![]() ,
,
∴当a=11时,y最大=297.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目