题目内容
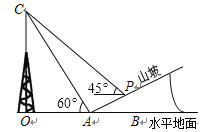
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为![]() (即tan∠PAB=
(即tan∠PAB=![]() ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
【答案】(50![]() -50)米.
-50)米.
【解析】试题分析:在直角△AOC中,利用三角函数即可求解;在图中共有三个直角三角形,即Rt△AOC、Rt△PCF、Rt△PAE,利用60°、45°以及坡度比,分别求出CO、CF、PE,然后根据三者之间的关系,列方程求解即可解决.
试题解析:过点P作PE⊥OB于点E,PF⊥CO于点F,

在Rt△AOC中,AO=200米,∠CAO=60°,
∴CO=AOtan60°=200![]() (米)
(米)
(2)设PE=x米,
∵tan∠PAB=![]() ,
,
∴AE=3x.
在Rt△PCF中,
∠CPF=45°,CF=200![]() -x,PF=OA+AE=200+3x,
-x,PF=OA+AE=200+3x,
∵PF=CF,
∴200+3x=200![]() -x,
-x,
解得x=50(![]() -1)米.
-1)米.
答:电视塔OC的高度是200![]() 米,所在位置点P的铅直高度是50(
米,所在位置点P的铅直高度是50(![]() -1)米.
-1)米.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目