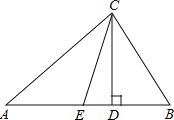
题目内容
【题目】如图,△ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图1,若点D为线段AC的中点,求证:AD=CE;
(2)如图2,若点D为线段AC上任意一点,试确定线段AD与CE的大小关系,并说明理由.

【答案】(1)详见解析;(2)AD=CE,理由详见解析.
【解析】
(1)根据等边三角形三线合一的性质即可求得∠DBC的度数,再根据BD=DE可求得∠E的度数,进而可求得∠CDE的度数,于是可判断CD与CE的关系,进一步即可得出结论;
(2)作DF∥AB,利用AAS可证△BDF≌△EDC,得BF=CE,再证AD=BF即可,而易证△DCF是等边三角形,所以CF=CD,再根据CA=CB,问题即得解决.
解:(1)∵△ABC是等边三角形,点D为线段AC的中点,
∴BD平分∠ABC,∠ABC=∠ACB=60°,∴∠DBE=30°,
∵BD=DE,∴∠E=∠DBE=30°,
∵∠DCE=180°﹣∠ACB=120°,
∴∠CDE=180°﹣120°﹣30°=30°,即∠E=∠CDE,
∴CD=CE,
∴AD=CE;
(2)作DF∥AB交BC于点F,如图2,
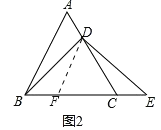
∵DF∥AB,∴∠DFC=∠ABC=60°,∠FDC=∠A=60°,
∴△DCF是等边三角形,
∴CF=CD,∵CA=CB,∴BF=AD,
∵∠DFC=60°,∴∠BFD=120°,
∵∠ACB=60°,∴∠ACE=120°,
∴∠BFD=∠ECD,
∵BD=DE,∴∠E=∠DBE,
在△BDF和△EDC中,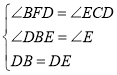 ,
,
∴△BDF≌△EDC(AAS),
∴BF=CE,
∴AD=CE.

 名校课堂系列答案
名校课堂系列答案【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本为________,样本容量为_______;
(2)在频数分布表中,a=______,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?

【题目】食品加工是一种专业技术,就是把原料经过人为处理形成一种新形式的可直接食用的产品,这个过程就是食品加工.比如用小麦经过碾磨、筛选、加料搅拌、成型烘干,成为饼干,就是属于食品加工的过程.下表给出了甲、乙、丙三种原料中的维生素A、B的含量(单位:g/kg).
原料甲 | 原料乙 | 原料丙 | |
维生素A的含量 | 4 | 6 | 4 |
维生素B的含量 | 8 | 2 | 4 |
将甲、乙、丙三种原料共100kg混合制成一种新食品,其中原料甲xkg,原料乙ykg.
(1)这种新食品中,原料丙的含量__________kg,维生素B的含量__________g;(用含![]() 、
、![]() 的式子表示)
的式子表示)
(2)若这种新食品中,维生素A的含量至少为440g,维生素B的含量至少为480g,请你证明:![]() .
.