题目内容
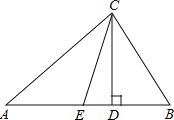
【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)
【答案】见解析
【解析】试题分析:(1)利用高的定义和互余得到∠BCD=90°-∠B,再根据角平分线定义得到∠BCE=![]() ∠ACB,接着根据三角形内角和定理得到∠ACB=180°-∠A-∠B,于是得到∠BCE=90°-
∠ACB,接着根据三角形内角和定理得到∠ACB=180°-∠A-∠B,于是得到∠BCE=90°-![]() (∠A+∠B),然后计算∠BCE-∠BCD得到∠ECD=
(∠A+∠B),然后计算∠BCE-∠BCD得到∠ECD=![]() (∠B-∠A),再把∠A=30°,∠B=50°代入计算即可;
(∠B-∠A),再把∠A=30°,∠B=50°代入计算即可;
(2)直接由(1)得到结论.
试题解析:(1)∵CD为高,∴∠CDB=90°,
∴∠BCD=90°-∠B,∵CE为角平分线,
∴∠BCE=![]() ∠ACB,而∠ACB=180°-∠A-∠B,
∠ACB,而∠ACB=180°-∠A-∠B,
∴∠BCE=![]() (180°-∠A-∠B)=90°-
(180°-∠A-∠B)=90°-![]() (∠A+∠B),
(∠A+∠B),
∴∠ECD=∠BCE-∠BCD =90°-![]() (∠A+∠B)-(90°-∠B)=
(∠A+∠B)-(90°-∠B)=![]() (∠B-∠A),
(∠B-∠A),
当∠A=30°,∠B=50°时,∠ECD=![]() ×(50°-30°)=10°;
×(50°-30°)=10°;
(2)由(1)得∠ECD=![]() (∠B-∠A).
(∠B-∠A).

练习册系列答案
相关题目

