Question

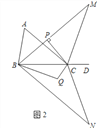
【题目】如图①，我们在“格点”直角坐标系上可以看到：要找或的长度，可以转化为求或的斜边长.

例如：从坐标系中发现：，，所以，，所以由勾股定理可得：.

(1)在图①中请用上面的方法求线段的长：______；在图②中：设，，试用，，，表示：______.

(2)试用(1)中得出的结论解决如下题目：已知：，，为轴上的点，且使得为等腰三角形，请求出点的坐标.

Answer 1

【答案】(1)，；(2)点或或或.

【解析】

（1）根据图①确定出AD与AE的长，利用勾股定理求出DE的长即可；

在图②中，由A与B的坐标表示出AC，BC，利用勾股定理表示出AB的长即可；

（2）①利用题中的方法，根据D与B坐标求出DB的长即可；

②设C，然后对、、进行分类讨论，根据A与B坐标，利用题中的方法列出方程，求出方程的解得到x的值，即可确定出C坐标.

(1)①从坐标系中发现：、，

∴，

∴由勾股定理得：；

②∵、

∴，，

(2)设点的坐标为，

当时，有，

即，解得.

当时，有，

即，解得或7，

当时，有，

即，解得，

综上点或或或.