Question

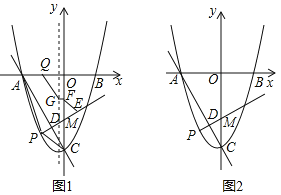
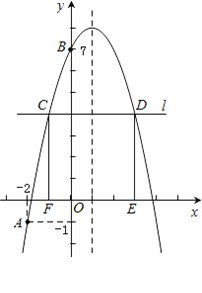
【题目】如图，已知二次函数y=-x2+bx+c的图象经过A（-2，-1），B（0，7）两点．

（1）求该抛物线的解析式及对称轴；

（2）当x为何值时，y＞0？

（3）在x轴上方作平行于x轴的直线l，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作x轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．

Answer 1

【答案】（1） y=-（x-1）2+8;对称轴为：直线x=1;（2） 当1-2＜x＜1+2时，y＞0；（3） C点坐标为：（-1，4）．

【解析】

（1）根据待定系数法求二次函数解析式，再用配方法或公式法求出对称轴即可；
（2）求出二次函数与x轴交点坐标即可，再利用函数图象得出x取值范围；
（3）利用正方形的性质得出横纵坐标之间的关系即可得出答案．

（1）∵二次函数y=-x2+bx+c的图象经过A（-2，-1），B（0，7）两点．

∴，解得：，

∴y=-x2+2x+7，

=-（x2-2x）+7，

=-[（x2-2x+1）-1]+7，

=-（x-1）2+8，

∴对称轴为：直线x=1．

（2）当y=0，

0=-（x-1）2+8，

∴x-1=±2，

x1=1+2，x2=1-2，

∴抛物线与x轴交点坐标为：（1-2，0），（1+2，0），

∴当1-2＜x＜1+2时，y＞0；

（3）当矩形CDEF为正方形时，

假设C点坐标为（x，-x2+2x+7），

∴D点坐标为（-x2+2x+7+x，-x2+2x+7），

即：（-x2+3x+7，-x2+2x+7），

∵对称轴为：直线x=1，D到对称轴距离等于C到对称轴距离相等，

∴-x2+3x+7-1=-x+1，

解得：x1=-1，x2=5（不合题意舍去），

x=-1时，-x2+2x+7=4，

∴C点坐标为：（-1，4）．