Question

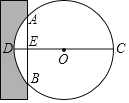
【题目】《九章算术》是我国古代著名数学著作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥DC于E，ED＝1寸，AB＝10寸，求直径CD的长．”则CD＝_______寸．

Answer 1

【答案】26

【解析】

连接OA构成直角三角形，先根据垂径定理，由DE垂直AB得到点E为AB的中点，由AB=10可求出AE的长，再设出圆的半径OA为x，表示出OE，根据勾股定理建立关于x的方程，求出方程的解即可得到x的值，即为圆的半径，把求出的半径代入即可得到答案．

解：连接OA，∵AB⊥CD，且AB=10，

∴AE=BE=5，

设圆O的半径OA的长为x，则OC=OD=x，

∵DE=1，

∴OE=x-1，

在直角三角形AOE中，根据勾股定理得：

x2-（x-1）2=52，化简得：x2-x2+2x-1=25，

即2x=26，

解得：x=13；

∴CD=26（寸）．

故答案为：26.