题目内容
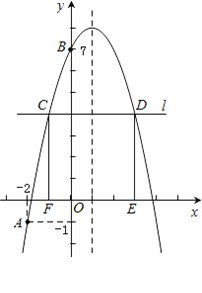
【题目】如图矩形COAB,点B(4,3),点H位于边BC上.

直线l1:2x﹣y+3=0
直线l2:2x﹣y﹣3=0
(1)若点N为l2上第一象限的点,△AHN为等腰Rt△,求N坐标.
(2)若把l1、l2上的点构成的图形称为图形V.已知矩形AJHI的顶点J在图形V上,I为平面系上的点,且J(x,y),求x的范围(写出过程).
【答案】(1)点N的坐标为(![]() ,
,![]() );(2,1);(
);(2,1);(![]() ,
,![]() );(2)x的取值范围为﹣
);(2)x的取值范围为﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() 或
或![]() ≤x≤2或
≤x≤2或![]() ≤x≤
≤x≤![]() .
.
【解析】
(1)分点A、H、N分别为直角时的三种情况,根据等腰直角三角形的性质,设点N的坐标利用全等三角形的关系求出x的值即可得到答案;
(2)当点J在l2上,分两种情况:点H与点B重合时与点C重合时,利用直角三角形斜边中线等于斜边的一半及勾股定理求出点J的坐标,即可得到取值范围,同样的方法求出点J在l1上时x的取值范围即可得到答案.
(1)①若点A为直角顶点时,点N在第一象限,连结AC,
如图1,∠AHB>∠ACB>45°,
∴△AHN不可能是等腰直角三角形,
∴点N不存在;
②若点H为直角顶点时,点N在第一象限,如图1,
过点N作MN⊥CB,交CB的延长线于点M,
则Rt△ABH≌Rt△HMN,
∴AB=HM=4,MN=HB,
设N(x,2x﹣3),则MN=x﹣4,
∴2x﹣3=4+3﹣(x﹣4),
x=![]() ,
,
∴N(![]() ,
,![]() );
);
③若点N为直角顶点时,点N在第一象限,如图2,
设N1(x,2x﹣3),
过点N1作N1G1⊥OA,交BC于点P1,
则Rt△AN1G1≌Rt△HM1P1,
∴AG1=N1P1=3﹣(2x﹣3),
∴x+3﹣(2x﹣3)=4,
x=2,
∴N1(2,1);
设N2(x,2x﹣3),
同理可得x+2x﹣3﹣3=4,
∴x=![]() ,
,
∴N2(![]() ,
,![]() );
);
综上所述,点N的坐标为(![]() ,
,![]() );(2,1);(
);(2,1);(![]() ,
,![]() );
);
(2)当点J在直线l2上时,
∵点J的横坐标为x,
∴J(x,2x﹣3),
当点H和点B重合时,H(4,3),
∴AH的中点G坐标为(2,3),
∵四边形AJHI是矩形,
∴∠AJB=90°,
∴JG=![]() AH=2,
AH=2,
∴(x﹣2)2+(2x﹣3﹣3)2=4,
∴x=![]() (点J在AB上方的横坐标)或x=2(点J在AB下方的横坐标),
(点J在AB上方的横坐标)或x=2(点J在AB下方的横坐标),
当点H和点C重合时,H(4,0),AH的中点G'坐标为(2,![]() ),
),
同理:JG'=![]() AH=
AH=![]() ,
,
∴(x﹣2)2+(2x﹣3﹣![]() )2=
)2=![]() ,
,
∴x=![]() (和点J在AB上方构成的四边形是矩形的横坐标)或x=
(和点J在AB上方构成的四边形是矩形的横坐标)或x=![]() (和点J在AB下方构成的四边形是矩形的横坐标)
(和点J在AB下方构成的四边形是矩形的横坐标)
∴![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤2.
≤x≤2.
当点J在l1上时,同理:﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() .
.
综上所述,x的取值范围为﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() 或
或![]() ≤x≤2或
≤x≤2或![]() ≤x≤
≤x≤![]() .
.



 优学名师名题系列答案
优学名师名题系列答案