Question

【题目】在平面直角坐标系中，抛物线y＝x2+x﹣4与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，作直线AC．

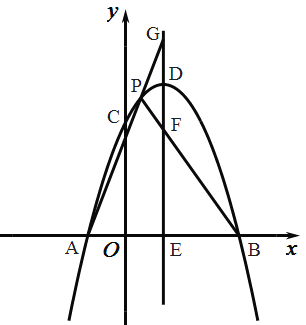
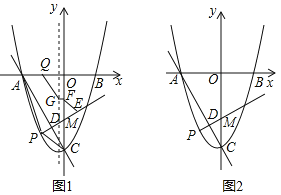
（1）如图1，点P是直线AC下方抛物线上的一点，连结PA，PC．过点P作PD⊥AC于点D，交y轴于点M，E是射线PD上的一点，Q是x轴上的一点，F是y轴上的一点，过F作该抛物线对称轴的垂线段，垂足为点G，连结EF，GQ．当△PAC面积最大时，求点P的坐标，并求EF+GQ+（FG+QA）的最小值；

（2）如图2，在（1）的条件下，将△CDM绕点D旋转得到△C'DM'，在旋转过程中，当点C'或点M′落在y轴上（不与点M、C重合）时，将△C'DM'沿射线PD平移得到△C″D'M″，在平移过程中，平面内是否存在点N，使得四边形OM″NC″是菱形？若存在，请直接写出所有符合条件的点N的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）P(﹣2，)，最小值为6；（2）存在，(3，-3)或(5，-5)

【解析】

（1）待定系数法求得直线AC的解析式为，运用二次函数最值求△PAC面积最大时对应的点P的坐标P(﹣2，)，作FQ′∥GQ交x轴于点Q′，在x轴上方以AQ′为斜边作Rt△AQ′T，使∠ATQ′＝90°，∠Q′AT＝30°，得到TQ′＝AQ′，从而有：EF+GQ+（FG+QA）＝EF+FQ′+TQ′，当T、Q′、F、E四点共线时，EF+GQ+（FG+QA）的值最小；易求得最小值为6；

（2）分两种情况：①当点C′落在y轴上时，可求得N1(3，﹣3)；②当点M′落在y轴上时，可求得N2(5，﹣5)．

解：（1）在抛物线y＝x2+x﹣4中，令x＝0，得y＝，

∴

令y＝0，得，解得x1＝﹣4，x2＝3，

∴A（﹣4，0），B（3，0）；

设直线AC的解析式为y＝kx+b，将A（﹣4，0），C（0，）分别代入得，解得，

∴直线AC的解析式为，

如图1，过点P作PH⊥x轴交直线AC于H，

设点P(m，)，H(m，)

∴＝，

∴＝＝，

∵，

∴当m＝﹣2时，S△PAC的最大值＝，此时P(﹣2，)，

∵PD⊥AC，

∴∠CDM＝∠COA＝90°，

∴tan∠ACO＝＝，

∴∠ACO＝30°，∠CMD＝∠CAO＝∠OME＝60°，

过点P作PL⊥y轴于L，∠PLM＝90°，∠MPL＝90°﹣∠CMD＝90°﹣60°＝30°，L(0，)，

∴，即：ML＝PLtan∠MPL＝2×tan30°＝，

∴，CM＝，CD＝CMsin∠CMD＝sin60°＝2

易得抛物线对称轴为x＝，

在OQ上截取QQ′＝FG，连接Q′F，在x轴上方过A作AK交y轴于K，使∠OAK＝30°，过Q′作Q′T⊥AK于T，则TQ′＝AQ′，

∵QQ′＝FG，QQ′//FG

∴四边形FGQQ′是平行四边形

∴FQ′＝GQ

∴EF+GQ+(FG+QA)＝EF+FQ′+TQ′，当T、Q′、F、E四点共线时，EF+GQ+(FG+QA)的值最小；

∵∠AKO＝60°＝∠CMD

∴AK∥PM

∴此时，ET⊥PM，ET//AC，四边形ADET是矩形

∴ET＝AD＝AC﹣CD＝8﹣2＝6

故EF+GQ+(FG+QA)的值最小值＝6．

（2）存在．∵△C'DM'沿射线PD平移得到△C″D'M″，且射线PD与x轴正方向夹角为30°，

∴平移后的△C″D′M″各顶点坐标与△C′DM′关系为：向右平移t个单位，向上平移t个单位；

①当点C′落在y轴上时，如图2，

∵DC′＝DC，

∴∠DC′C＝∠DCC′＝30°，∠CDC′＝120°，

∴∠C′DM＝∠CDC′﹣∠CDM＝120°﹣90°＝30°.

∵∠DC′M′＝∠DCM＝30°，

∴∠C′DM＝∠DC′M′，

∴C′M′∥PM，且C′M′与PM之间的距离＝1.

∵四边形OM″NC″是菱形，

∴ON与C″M″互相垂直平分，过点O作ON⊥PD，

∵∠CON＝90°﹣∠ODH＝30°

∴OH＝OMcos30°＝×＝4，易求O到C″M″的距离为3，

∴ON＝6，

∴N1(3，﹣3)；

②当点M′落在y轴上时，如图3，

易知：DM＝DM′，∠DMM′＝∠DM′M＝60°，

∴△DMM′为等边三角形，

∴∠MDM′＝60°＝∠C′M′D，

∴C′M′//PD，

∴C″M″//PD.

由①知：C″M″与PD间距离为1，∴O到C″M″的距离＝4+1＝5，

∵ON与C″M″互相垂直平分，

∴ON＝10，

∴N2(5，﹣5).

故点N的坐标为：N1(3，﹣3)，N2(5，﹣5)．