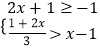题目内容
【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由 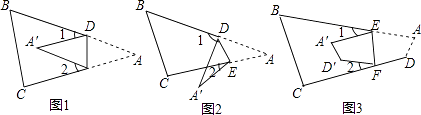
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.
【答案】
(1)解:图1中,2∠A=∠1+∠2,
理由是:∵沿DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
如图2,2∠A=∠1﹣∠2.
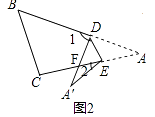
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2
(2)解:如图3,
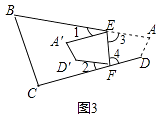
根据翻折的性质,∠3= ![]() (180﹣∠1),∠4=
(180﹣∠1),∠4= ![]() (180﹣∠2),
(180﹣∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+ ![]() (180﹣∠1)+
(180﹣∠1)+ ![]() (180﹣∠2)=360°,
(180﹣∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°
【解析】根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;(1)运用三角形的外角性质即可解决问题;(2)先根据翻折的性质表示出∠3、∠4,再根据四边形的内角和定理列式整理即可得解.
【考点精析】关于本题考查的三角形的内角和外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案