题目内容
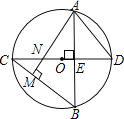
【题目】已知四边形ABCD为菱形，连接BD，点E为菱形ABCD外任一点．
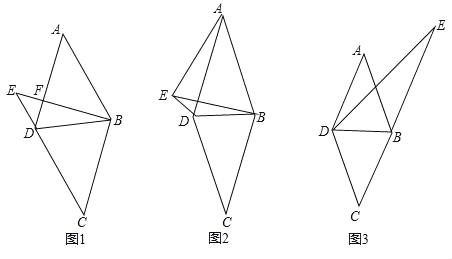
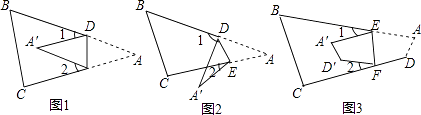
（1）如图（1），若∠A=45°，AB=
，点E为过点B作AD边的垂线与CD边的延长线的交点，BE，AD交于点F，求DE的长．
（2）如图（2），若2∠AEB=180°﹣∠BED，∠ABE=60°，求证：BC=BE+DE
（3）如图（3），若点E在的CB延长线上时，连接DE，试猜想∠BED，∠ABD，∠CDE三个角之间的数量关系，直接写出结论
【答案】（1）2
﹣
．（2）证明参见解析；（3）2∠ABD=∠BED+∠CDE．
【解析】
试题分析：（1）首先证明△AFB与△EFD为等腰直角三角形，然后在△ABF中依据勾股定理可求得BF和AF的长，从而得到DF的长，然后在Rt△EDF中，可求得DE的长；（2）延长DE至K，使EK=EB，连结AK．首先证明∠AEB=∠AEK，然后依据SAS证明△AEB≌△AEK，由全等三角形的性质及等边三角形的判断定理可证明△AKD为等边三角形，于是得到KD=BC，通过等量代换可得到问题的答案；（3）记AB与DE的交点为O．首先证明依据菱形的性质可得到∠ABC=2∠ABD，然后依据平行四边形的性质可证明∠CDE=∠BOE，最后依据三角形外角的性质可得到问题的答案．
试题解析：（1）如图1所示：
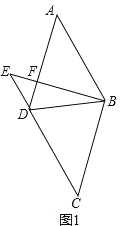
∵四边形ABCD为菱形，∴AD=AB=
，AB∥CD．∴∠A=∠ADE=45°．∵AD⊥BE，∴∠AFB=DFE=90°．∴△AFB与△EFD为等腰直角三角形．∴BF2+AF2=AB2，即：2BF2=6，∴BF=AF=
．∵△EFD为等腰直角三角形，∴EF=DF=AD﹣AF=﹣．∴DE=
EF=（﹣）=2﹣．（2）如图2所示：延长DE至K，使EK=EB，联结AK．
∵2∠AEB=180°﹣∠BED，∴∠BED=180°﹣2∠AEB=180°﹣∠AEB﹣∠AEK．∴∠AEB=∠AEK．在△AEB和△AEK中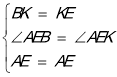
，∴△AEB≌△AEK．∴∠K=∠ABE=60°，Ak=AB．又∵AB=AD，∴AK=AD．∴△AKD为等边三角形．∴KD=AD．∴KD=BC．∵KD=KE+DE，∴CB=EB+DE．（3）如图3所示：记AB与DE的交点为O．
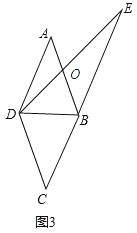∵四边形ABCD为菱形，∴AB∥DC，∠ABC=2∠ABD．∴∠CDE=∠BOE．∵∠ABC=∠BED+∠EOB，∴2∠ABD=∠BED+∠CDE．
