题目内容
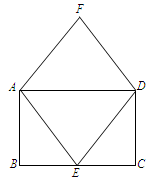
如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )


| A.2cm | B. cm cm | C.4cm | D.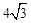 cm cm |
A.
试题分析:设CD=AB=x,则
∵点E,F分别是CD和AB的中点,∴DE=AF=
 .
.∵现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,∴AG=AB=x,∠AGH=∠B=900.
∵HG的延长线恰好经过点D,∴∠AGD=∠AGH=900.
在Rt△AGD中,AD=4cm,AG=x,根据勾股定理得
 .
.易得△DEG∽△AGD,∴
 ,即
,即 ,解得
,解得 .
.故选A.

练习册系列答案
相关题目

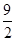 ,
,