题目内容
如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE

(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.

(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.
(1)∠CAE=30°;(2)∠FAE=90°,四边形AFCE是矩形
解:∵△ABC是等边三角形,且D是BC中点,
∴DA平分∠BAC,即∠DAB=∠DAC=30°;
∵△DAE是等边三角形,
∴∠DAE=60°;
∴∠CAE=∠DAE-∠CAD=30°;
(2)证明:∵△BAC是等边三角形,F是AB中点,
∴CF⊥AB;
∴∠BFC=90°
由(1)知:∠CAE=30°,∠BAC=60°;
∴∠FAE=90°;
∴AE∥CF;
∵△BAC是等边三角形,且AD、CF分别是BC、AB边的中线,
∴AD=CF;
又AD=AE,
∴CF=AE;
∴四边形AFCE是平行四边形;
∵∠FAE=90°,
∴四边形AFCE是矩形.

练习册系列答案
相关题目


 和
和 的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.
的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.


 cm
cm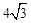 cm
cm )n
)n