题目内容
如图,四边形ABCD为矩形,四边形AEDF为菱形.
(1)求证:△ABE≌△DCE;
(2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.
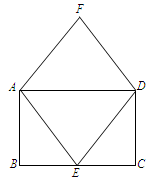
(1)求证:△ABE≌△DCE;
(2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.

(1)证明见解析;(2)当BC=2AB时,菱形AEDF为正方形.理由见解析.
试题分析:(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,根据菱形的四条边都相等可得AE=DE,然后利用“HL”证明Rt△ABE和Rt△DCE全等即可;
(2)BC=2AB时,菱形AEDF为正方形.根据全等三角形对应边相等可得BE=CE,然后求出AB=BE,从而求出∠BAE=∠AEB=45°,同理可得∠DEC=45°,然后求出∠AED=90°,最后根据有一个角是90°的菱形是正方形判断.
(1)证明:∵四边形ABCD为矩形,
∴∠B=∠C=90°,AB=DC,
∵四边形AEDF为菱形,
∴AE=DE,
在Rt△ABE和Rt△DCE中,
 ,
,∴Rt△ABE≌Rt△DCE(HL);
(2)解:当BC=2AB时,菱形AEDF为正方形.
理由:∵Rt△ABE≌Rt△DCE,
∴BE=CE,∠AEB=∠DEC,
又∵BC=2AB,
∴AB=BE,
∴∠BAE=∠AEB=45°,
同理可得,∠DEC=45°,
∵∠AEB+∠AED+∠DEC=180°,
∴∠AED=180°-∠AEB-∠DEC=90°,
∴菱形AEDF是正方形.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目


 中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.
中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.


 cm
cm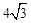 cm
cm PC; ④PE+PF=PC。其中正确的是( )
PC; ④PE+PF=PC。其中正确的是( )
 )n
)n