题目内容
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.

求证:四边形BECF是平行四边形.

详见解析.
试题分析:本题是关于平行四边形的判定,判定方法有五种:?定义:两组对边分别平行的四边形是平行四边形;?两组对边分别相等的四边形是平行四边形?一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;⑤两组对角分别相等的四边形是平行四边形.找出合适的条件即可,此种类型题常有多种证法.举一证法如下:
试题解析:证明:∵BE⊥AD,BE⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
 ,
,∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,BE⊥AD,
∴BE∥CF
∴四边形BECF是平行四边形.

练习册系列答案
相关题目

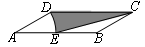
 中,
中, ,
, 为平面内一动点,
为平面内一动点, ,
, ,其中a,b为常数,且
,其中a,b为常数,且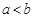 .将
.将 沿射线
沿射线 方向平移,得到
方向平移,得到 ,点A、B、D的对应点分别为点F、C、E.连接
,点A、B、D的对应点分别为点F、C、E.连接 .
. ,求
,求 的式子表示);
的式子表示); ,当线段
,当线段 的大小为__________;当线段
的大小为__________;当线段 的式子表示).
的式子表示).



 cm
cm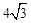 cm
cm ,若直线l满足:(1)点D到直线l的距离为
,若直线l满足:(1)点D到直线l的距离为 ,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
