Question

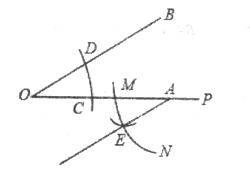
【题目】如图，在平行四边形ABCD中，AC与BD相交于点O，∠AOB=60°，BD=4，将△ABC沿直线AC翻折后，点B落在点E处，那么S△AED=______

Answer 1

【答案】

【解析】

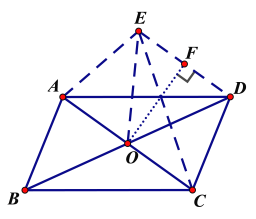
根据题意画出翻折后的图形，连接OE、DE，先证明△OED是等边三角形，再利用同底等高的三角形面积相等，说明S△AED=S△OED，作OF⊥ED于F，求出△OED的面积即可得出结果.

解：如图，△AEC是△ABC沿AC翻折后的图形，连接OE、DE，

∵四边形ABCD是平行四边形，

∴OB=OD=BD=2，

∵△AEC是△ABC沿AC翻折后的图形，∠AOB=60，

∴∠AOE=60，OE=OB，

∴∠EOD=60，OE=OD，

∴△OED是等边三角形，

∴∠DEO=∠AOE=60，ED=OD=2，

∴ED∥AC，

∴S△AED=S△OED，

作OF⊥ED于F，DF=ED=1，

∴OF==，

∴S△OED=ED·DF=

∴S△AED=.

故答案为：.