题目内容
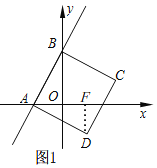
【题目】如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.

【答案】(1)A(-2,0),B(0,4),D(2,-2);(2)M(5,0).
【解析】
(1)由于一次函数y=2x+4的图象与x、y轴分别交于点A、B,所以利用函数解析式即可求出A、B两点的坐标,然后作DF⊥x轴于点F,由四边形ABCD是正方形可以得到∠BAD=∠AOB=∠AFD=90,AB=AD,接着证明△BAO≌△ADF,最后利用全等三角形的性质可以得到DF=AO=2,AF=BO=4,从而求出点D的坐标;
(2) 过点C作CG⊥y轴于G,连接OC,作CM⊥OC交x轴于M,用求点D的方法求得点C的坐标为(4,2),得出OC=2![]() ,由A、B的坐标得到AB=2
,由A、B的坐标得到AB=2![]() ,从而OC=AB=AD,根据△ADE与△COM全等,利用全等三角形的性质可知OM=AE,即OA=EM=2,利用C、D的坐标求出直线CD的解析式,得出点E的坐标,根据EM=2,即可求出点M的坐标.
,从而OC=AB=AD,根据△ADE与△COM全等,利用全等三角形的性质可知OM=AE,即OA=EM=2,利用C、D的坐标求出直线CD的解析式,得出点E的坐标,根据EM=2,即可求出点M的坐标.
解:(1)∵一次函数y=2x+4的图象与x,y轴分别相交于点A,B,
∴A(-2,0),B(0,4),
∴OA=2,OB=4,
如图1,过点D作DF⊥x轴于F,
∴∠DAF+∠ADF=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠DAF+∠BAO=90°,
∴∠ADF=∠BAO,
在△ADF和△BAO中,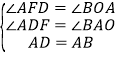 ,
,
∴△ADF≌△BAO(AAS),
∴DF=OA=2,AF=OB=4,
∴OF=AF-OA=2,
∵点D落在第四象限,
∴D(2,-2);
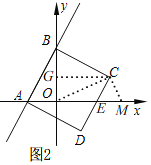
(2)如图2,过点C作CG⊥y轴于G,连接OC,作CM⊥OC交x轴于M,
同(1)求点D的方法得,C(4,2),
∴OC=![]() =2
=2![]() ,
,
∵A(-2,0),B(0,4),
∴AB=2![]() ,
,
∵四边形ABCD是正方形,
∴AD=AB=2![]() =OC,
=OC,
∵△ADE与△COM全等,且点M在x轴上,
∴△ADE≌△OCM,
∴OM=AE,
∵OM=OE+EM,AE=OE+OA,
∴EM=OA=2,
∵C(4,2),D(2,-2),
∴直线CD的解析式为y=2x-6,
令y=0,
∴2x-6=0,
∴x=3,
∴E(3,0),
∴OM=5,
∴M(5,0).
故答案为:(1)A(-2,0),B(0,4),D(2,-2);(2)M(5,0).