Question

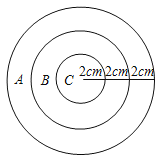
【题目】已知二次函数y1＝mx2﹣nx﹣m+n（m＞0）．

（Ⅰ）求证：该函数图象与x轴必有交点；

（Ⅱ）若m﹣n＝3，

（ⅰ）当﹣m≤x＜1时，二次函数的最大值小于0，求m的取值范围；

（ⅱ）点A（p，q）为函数y2＝|mx2﹣nx﹣m+n|图象上的动点，当﹣4＜p＜﹣1时，点A在直线y＝﹣x+4的上方，求m的取值范围．

Answer 1

【答案】（Ⅰ）见解析; （Ⅱ）（ⅰ）；（ⅱ）或

【解析】

（Ⅰ）利用一元二次方程根的情况判断抛物线与x轴的交点情况；

（Ⅱ）（ⅰ）根据已知条件得到抛物线解析式为：＝mx2﹣（m﹣3）x﹣3．由此求得抛物线与x轴的交点坐标，然后根据抛物线的增减性求得m的取值范围；

（ⅱ）根据二次函数图象与不等式间的转化关系解答．

（Ⅰ）∵△＝（﹣n）2﹣4m（﹣m+n）＝（n﹣2m）2≥0，

∴该函数图象与x轴必有交点；

（Ⅱ）（ⅰ）∵m﹣n＝3，

∴n＝m﹣3．

∴

＝mx2﹣（m﹣3）x﹣3．

当y1＝0时，mx2﹣（m﹣3）x﹣3＝0，

解得x1＝1，

∴二次函数图象与x轴交点为（1，0）和（ ，0）

∵当﹣m≤x＜1时，二次函数的最大值小于0，

∴

又∵m＞0，

∴；

（ⅱ），m﹣n＝3，

∴当或x＞1时，y2＝mx2﹣（m﹣3）x﹣3，

当时，y2＝﹣mx2+（m﹣3）x+3．

∵当﹣4＜p＜﹣1时，点A在直线y＝﹣x+4上方，

∴当，即m＞3时，有m×（﹣1）2﹣（m﹣3）×（﹣1）﹣3≥﹣（﹣1）+4，

解得．

当，即m时，有﹣m×（﹣1）2+（m﹣3）×（﹣1）+3≥﹣（﹣1）+4

且﹣m×（﹣4）2+（m﹣3）×（﹣4）+3≥﹣（﹣4）+4，

∴．

又∵m＞0

∴．

综上，或．