题目内容
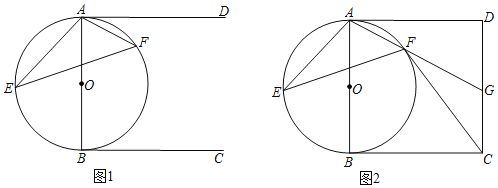
【题目】已知,AB是⊙O的直径,E、F是⊙O上的点,连接AE、AF、EF,BC是⊙O的切线,过点A作AD∥BC.
(1)如图1,求证:∠DAF=∠AEF;
(2)如图2,若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若FC=BC=4,求AG的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)如图1,连接BF,根据切线的性质得到∠ABC=90°,根据圆周角定理得到∠AFB=90°,推出∠ABF=∠DAF,等量代换即可得到结论;
(2)如图2,连接OF,OC,根据全等三角形的性质得到∠OFC=∠ABC=90°,∠BOC=∠FOC,推出∠BAG=∠BOC,得到四边形ABCD是正方形,于是得到AB=CD,∠D=90°,AB∥CD,根据全等三角形的性质得到AD=BC=4,DG=BO=2,根据勾股定理得到AG=![]() =
=![]() .
.
(1)证明:如图1,连接BF,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
∵AD∥BC,
∴∠DAB=90°,
∴∠DAF+∠BAF=90°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠ABF+∠BAF=90°,
∴∠ABF=∠DAF,
∵∠AEF=∠ABF,
∴∠AEF=∠DAF;
(2)解:如图2,连接OF,OC,
在△CBO与△CFO中,
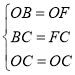 ,
,
∴△CBO≌△CFO(SSS),
∴∠OFC=∠ABC=90°,∠BOC=∠FOC,
∵OA=OF,
∴∠OAF=∠OFA,
∵∠OAF=![]() ,∠BOC=
,∠BOC=![]() ,
,
∴∠BAG=∠BOC,
∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=BC,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=CD,∠D=90°,AB∥CD,
∴∠BAG=∠DGA=∠BOC,
在△ADG与△CBO中,
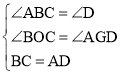 ,
,
∴△ADG≌△CBO(AAS),
∴AD=BC=4,DG=BO=2,
∴AG=![]() =2
=2![]() .
.