题目内容
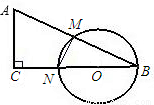
已知如图,△ABC中,∠C=90°,AC=3,BC=3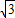 ,以BC边上点O为圆心,以OB为半径的圆分别交边AB、BC于点M、N.连接MN.
,以BC边上点O为圆心,以OB为半径的圆分别交边AB、BC于点M、N.连接MN.(1)请你探究:四条线段AB、BM、BC、BN之间的关系,并证明你的结论;
(2)若M是AB边的中点,请你判断CM与⊙O的位置关系,并说明理由;
(3)设⊙O的半径为r,若改变点O在BC上的位置,试探究当半径r满足什么条件时,⊙O与边AC只有一个公共点.(直接写出答案)
【答案】分析:(1)根据已知利用有两组角相等的两个三角形相似得到△BMN∽△BCA,从而不难得到四个边之间的关系;
(2)连接OM,根据已知利用三角函数可得到△ACM是等边三角形,进而可推出OM⊥CM,因为OM是圆的半径,所以CM与⊙O相切;
(3)当圆以BC的一半为半径或与边AC相切时,⊙O与边AC只有一个公共点.
解答: 解:(1)
解:(1)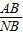 =
=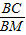
∵BN是直径,
∴∠NMB=90°∠ACB=90°
∴∠NMB=∠ACB,∠B=∠B
∴△BMN∽△BCA
∴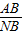 =
= ;(3分)
;(3分)
(2)连接OM
在Rt△ACB中,tanB=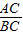 =
=
∴∠B=30°
∴∠A=90°-30°=60°
∵M是AB的中点
∴MC=MA= AB
AB
∴△ACM是等边三角形
∴∠CMA=60°
∴∠OMB=∠B=30°
∴∠CMO=180°-60°-30°=90°
∴OM⊥CM
∴CM是⊙O的切线;(4分)
(3) ≤r≤2
≤r≤2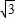 (2分)
(2分)
点评:此题主要考查学生对切线的判定,相似三角形的判定及圆与直线的位置关系等知识点的综合运用能力.
(2)连接OM,根据已知利用三角函数可得到△ACM是等边三角形,进而可推出OM⊥CM,因为OM是圆的半径,所以CM与⊙O相切;
(3)当圆以BC的一半为半径或与边AC相切时,⊙O与边AC只有一个公共点.
解答:
 解:(1)
解:(1)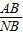 =
=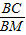
∵BN是直径,
∴∠NMB=90°∠ACB=90°
∴∠NMB=∠ACB,∠B=∠B
∴△BMN∽△BCA
∴
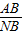 =
= ;(3分)
;(3分)(2)连接OM
在Rt△ACB中,tanB=
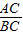 =
=
∴∠B=30°
∴∠A=90°-30°=60°
∵M是AB的中点
∴MC=MA=
 AB
AB∴△ACM是等边三角形
∴∠CMA=60°
∴∠OMB=∠B=30°
∴∠CMO=180°-60°-30°=90°
∴OM⊥CM
∴CM是⊙O的切线;(4分)
(3)
 ≤r≤2
≤r≤2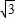 (2分)
(2分)点评:此题主要考查学生对切线的判定,相似三角形的判定及圆与直线的位置关系等知识点的综合运用能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
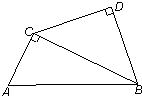 已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC=
已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC= 7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当
7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当 已知如图,△ABC中,BD⊥AC于D,tanA=
已知如图,△ABC中,BD⊥AC于D,tanA= 已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.
已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.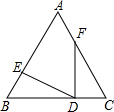 已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )
已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )