题目内容
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?
【答案】(1)-![]() x+90;(2)-
x+90;(2)-![]() x+90;
x+90;![]() x-50;x-80;10x-2000;(3)将每间客房的日租金定为200元,才能使度假村获得最大日收益.最大日收益是4800元.
x-50;x-80;10x-2000;(3)将每间客房的日租金定为200元,才能使度假村获得最大日收益.最大日收益是4800元.
【解析】
(1)判断出y与x的函数关系为一次函数关系,再根据待定系数法求出函数解析式;
(2)根据题意可用代数式求出的客房数和未出租客房数即可.
(3)租出的客房的利润减去未租客房的清洁费,即为公司日收益,再利用二次函数的性质求解可得.
解:(1)由表格知,每天的租赁价每增加20元,每天租出的客房少5辆,
所以y与x满足一次函数关系,设y=kx+b,
则![]() ,
,
解得: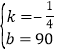 ,
,
∴y=-![]() x+90;
x+90;
(2)当每间客房日租金x元时,租出的客房数为-![]() x+90,租出每间客房的日收益为(x-80)元;
x+90,租出每间客房的日收益为(x-80)元;
未租出的客房数为40-(-![]() x+90)=
x+90)=![]() x-50,所有未租出的客房每日的维护费40(
x-50,所有未租出的客房每日的维护费40(![]() x-50)=10x-2000;
x-50)=10x-2000;
故答案为:-![]() x+90;
x+90;![]() x-50;x-80;10x-2000;
x-50;x-80;10x-2000;
(3)设公司获得的日收益为w,
则w=(x-80)(-![]() x+90)-(10x-2000)
x+90)-(10x-2000)
=-![]() x2+100x-5200
x2+100x-5200
=-![]() (x-200)2+4800(x≥200),
(x-200)2+4800(x≥200),
∵当x≥200时,w随x的增大而减小,
∴当x=200时,w取得最大值,最大值为4800,
答:将每间客房的日租金定为200元,才能使度假村获得最大日收益.最大日收益是4800元.

【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
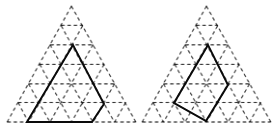
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).