题目内容
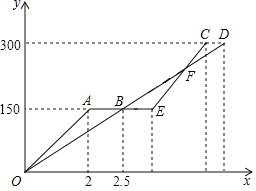
【题目】在平面直角坐标系
中，以直线
向上的方向为新坐标系
轴的正方向，过点
作一与新轴垂直的直线，垂足是点
，该直线向上的方向为新
轴的正方向，由此建立新的坐标系
.
(1)新轴所在直线在坐标系中的表达式是什么?
(2)点
在坐标系中坐标是
，在坐标系中的坐标是多少?
【答案】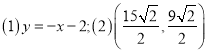
【解析】
（1）通过直线
的交点和等腰直角三角形的性质得出过（-2，0）的直线也过
，然后用待定系数法即可求出直线的表达式
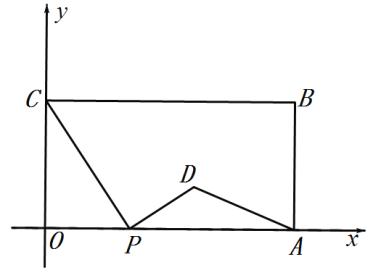
（2）过点P作PF⊥y轴于F，
于点G，
于点H，交y轴于点E，先利用待定系数法求出PH的表达式，然后利用等腰直角三角形的性质即可得出答案．
（1）如图
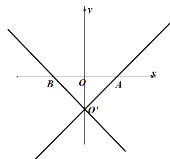
当
时，
，
∴
当
时，
，
∴
∴
为等腰直角三角形
∴过（-2，0）的直线也过
设直线
的解析式为
将
代入得
解得
∴
（2）过点P作PF⊥y轴于F， 于点G， 于点H，交y轴于点E
∴
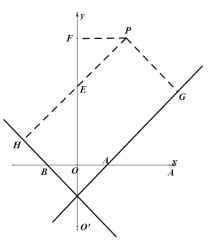
均为等腰直角三角形
设PH的直线方程为
将点
代入得
∴
∴
∴点P坐标系
中的坐标是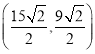
练习册系列答案
相关题目
