题目内容
【题目】如图,锐角![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一点,以
上的一点,以![]() 为边作
为边作![]() ,使
,使![]() ,
,![]() .
.
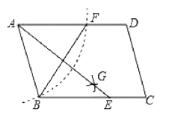
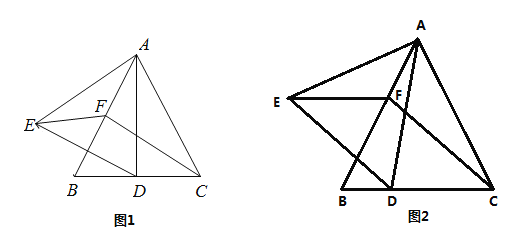
(1)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() (如图①)
(如图①)
①请直接写出![]() 与
与![]() 的数量关系;
的数量关系;
②试判断四边形![]() 的形状,并证明;
的形状,并证明;
(2)若![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() (如图②),那么(1)②中的结论是否任然成立?若成立,请给出证明,若不成立,请说明理由.
(如图②),那么(1)②中的结论是否任然成立?若成立,请给出证明,若不成立,请说明理由.
【答案】(1)①![]() ; ② 平行四边形,证明见解析;(2)成立,证明见解析.
; ② 平行四边形,证明见解析;(2)成立,证明见解析.
【解析】
(1)①根据![]() ,两角有公共角
,两角有公共角![]() ,可证
,可证![]() ;
;
②连接EB,证明△EAB≌△DAC,可得![]() ,再结合平行线的性质和等腰三角形的判定定理可得EF=DC,由此可根据一组对边平行且相等的四边形是平行四边形证明四边形
,再结合平行线的性质和等腰三角形的判定定理可得EF=DC,由此可根据一组对边平行且相等的四边形是平行四边形证明四边形![]() 为平行四边形.
为平行四边形.
(2)根据![]() ,可证明△AED和△ABC为等边三角形,再根据ED∥FC结合等边三角形的性质,得出∠AFC=∠BDA,求证△ABD≌△CAF,得出ED=CF,进而求证四边形EDCF是平行四边形.
,可证明△AED和△ABC为等边三角形,再根据ED∥FC结合等边三角形的性质,得出∠AFC=∠BDA,求证△ABD≌△CAF,得出ED=CF,进而求证四边形EDCF是平行四边形.
解:(1)①![]() ,理由如下:
,理由如下:
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②证明:如下图,连接EB,
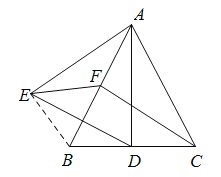
在△EAB和△DAC中
∵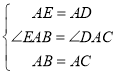
∴△EAB≌△DAC(SAS)
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴四边形![]() 为平行四边形;
为平行四边形;
(2)成立;理由如下:
理由如下:
∵![]() ,
,
∴![]() ,
,
∵AE=AD,AB=AC,
∴△AED和△ABC为等边三角形,
∴∠B=60°,∠ADE=60°,AD=ED,
∵ED∥FC,
∴∠EDB=∠FCB,
∵∠AFC=∠B+∠BCF=60°+∠BCF,∠BDA=∠ADE+∠EDB=60°+∠EDB,
∴∠AFC=∠BDA,
在△ABD和△CAF中,
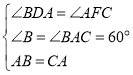
∴△ABD≌△CAF(AAS),
∴AD=FC,
∵AD=ED,
∴ED=CF,
又∵ED∥CF,
∴四边形EDCF是平行四边形.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目